HSS Splice Design | Part 3: Rectangular HSS Bolted End-Plate Connections Under Bending Moment

by Jeffrey A. Packer and Ian G. Kennedy
Department of Civil & Mineral Engineering, University of Toronto, Ontario, Canada
December 2025

Bolted end-plate connections are a straightforward and cost-effective method to join both rectangular and round HSS members end-to-end. For rectangular HSS, connections either bolt around all four sides of the HSS or just two, with the former being more common, as it typically allows for thinner end-plates (Figure 1). Depending on the structural system, different loading conditions are possible; applications in columns and towers experience predominantly axial loads, whereas the use within beams and moment (e.g. Vierendeel) frames will subject connections largely to bending. The vast majority of research has historically focused on the axial tension load case, with design models for both two- and four-sided rectangular HSS bolted end-plate connections in tension presented in the AISC Design Guide 24 (DG24) (Packer and Olson, 2024). However, neither DG24 nor the AISC Manual (AISC, 2023) give any guidance for the design of these connections under bending.

Past research on rectangular HSS connections in bending is limited to 26 tests on 4-bolt connections (with a pair of bolts above and below the two HSS flanges) and 8-bolt connections (with a pair of bolts adjacent to each of the four HSS sides) by Wheeler et al. (1998). On the basis of experimental results, yield-line analysis, and finite element numerical studies, design models for these two types of connections were developed. The design method relies on the two connected HSS members being of similar size, and the end-plate blanking off the end of the HSS member (i.e. a “ring flange” is not used and there is no substantial hole at the center of the end-plate). Key and Syam (2014) later implemented this design method in a design guide but stressed that it was only applicable for either: (i) a two-sided connection with a line of two or more bolts above one HSS flange, accompanied by a mirrored layout beneath the other HSS flange; or (ii) a four-sided connection with two bolts adjacent to each HSS side. In view of the constraint on (ii), a modified way of handling other bolting arrangements is proposed below.

When rectangular HSS bolted end-plate connections are subjected to bending moments, the end-plates tend to rotate, creating two potential failure modes: when plates are thin, end-plate plastic hinging will govern, but when plates are thick, the connection will instead be governed by bolt fracture. Wheeler et al. (1998) found that, for two-sided connections, three different yield line patters tend to develop in the end plates, shown in Figure 2. However, DG24 notes that bolts should not be positioned outside the HSS dimension, else the bolt forces will not be evenly distributed. Applying this practical consideration to the Wheeler et al. (1998) design model eliminates the most complex yield line pattern (mode 3), simplifying the approach. For four-sided connections, the presence of bolts around the entire cross-section creates a global yielding mechanism within the end-plates, similar to round HSS bolted end-plate connections in bending (Fidalgo and Packer, 2023).

During bending, tension and compression regions will be created within the end-plate connection. While compression is transferred through contact between the end-plates, tension is carried by the bolts, thus the critical bolts are those located on the tension side of the connection. For two-sided connections, this corresponds to one of the bolt lines, so the number of tension bolts (n_T) can be taken simply as half the total number of bolts. However, this is not the case in four-sided connections. Research on round HSS has shown that, during bending, the center of rotation is located along an axis at the extreme compression fiber of the HSS (Fidalgo and Packer, 2023). As a result, about one third of the bolts experience no change in bolt force (i.e. the compressive region), one third experience increased bolt forces (i.e. the intermediate region), and one third experience maximum bolt forces (i.e. the tensile region). These findings inspired the design model for round HSS connections, where an “effective” number of bolts is taken as one third of the total (STI, 2023). For four-sided rectangular HSS connections, taking n_T equal to the number of bolts along only the extreme tension side is overly conservative, as it does not consider the partial contributions of the bolts located along the sides normal to the axis of moment application. These connections are more analogous to the round HSS scenario, thus n_T is taken as the total number of bolts divided by three, for four-sided connections. Examples of determining n_T for different bolt layouts are shown in Figure 3.

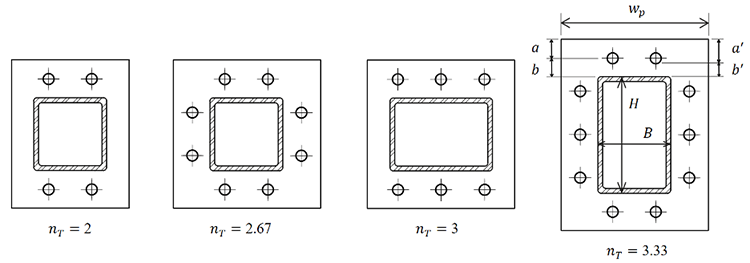
The design equations of Wheeler et al. (1998) are based on the linear yield-line patterns shown in Figure 2, thus it is only valid for two-sided rectangular HSS end-plate connections. Given that the four-sided connections are more common and often more economical, the model is expanded to apply to four-sided connections as well. This is done by considering the number of tension bolts (n_T) from a four-sided connection as a single row in the tensile region, which would allow the linear yield line patterns to develop across the full plate width (w_p). This “effective” two-sided connection can now be evaluated using the T-stub model for two-sided bolted rectangular HSS connections under bending by Wheeler et al. (1998). This process follows a similar conversion from round HSS to two-sided bolted rectangular HSS for end-plate connections under bending (STI, 2023).

Bending Moment Design Method

When the design model of Wheeler et al. (1998) was published, the prying effect model in the AISC Manual Part 9 and other technical standards used the plate nominal yield stress, F_yp. Consequently, the available moment capacity was calculated using this parameter. However, the current AISC Manual Part 9 (AISC, 2023) now uses the plate nominal tensile stress, F_up, which has been shown to provide more accurate predictions of the capacity of rectangular HSS in tension and round HSS in both tension and bending (Thornton, 2017; Fidalgo and Packer, 2024). A reliability study was conducted by the authors for the rectangular HSS end-plate connection nominal equations by Wheeler et al. (1998), with F_up used in lieu of F_yp. This analysis used a target reliability index of 4.0, as given in the AISC 360 Commentary to Section B3 (AISC, 2022) for low-ductility connections and supported by ASCE 7 (2022). Using a first-order reliability method (FORM), it was shown that a resistance factor of φ = 0.75 meets the target reliability index, therefore providing an adequate degree of safety. The nominal expressions by Wheeler et al. (1998) also feature the bolt yield stress, F_yb, an uncommon parameter in design. In ASTM F3125 (2025), the specified minimum yield stress of ASTM Grade A325 bolts is 77% of their nominal tensile stress, which is hence incorporated within the design equations. The available moment capacity (M_available) can therefore be calculated for LRFD as the minimum of Eq. (1), for when bolt failure governs the design, and Eq. (2), for when plate failure governs the design. The limits of applicability for the plate thickness (Eq. (3)) and the HSS height/width (Eq. (4)) must be met for these nominal equations to apply, as the model decreases in accuracy when plates are excessively thick or the HSS is small. Variables are defined below, with some shown in Figure 3.

In Eqs. (1) to (4):
a      = plate edge to bolt center distance (see Fig. 3)        (in.)
a’     = a + d_b/2        (in.)
b      = bolt center to HSS face distance        (in.)
b’     = b – d_b/2 (see Fig. 3)        (in.)
B      = HSS width dimension (see Fig. 3)        (in.)
B_t     = specified minimum tensile strength of one bolt        (kips)
d_b    = bolt diameter        (in.)
H      = HSS height dimension (see Fig. 3)        (in.)
F_up   = ultimate tensile strength of plate material        (ksi)
F_ub   = ultimate tensile strength of bolt material        (ksi)
n_T      = number of tension bolts        (-)
t_p      = end-plate thickness        (in.)
w_p    = end-plate width        (in.)

Combined Tension and Bending Design Method

In the case of truss chord members and moment-resisting frames, bolted HSS end-plate connections may be subjected to combined tension and bending loading, either through the application of separate actions or by eccentric axial loads. Research on round HSS has shown that a linear lower bound interaction curve for combined utilization provides a good estimate of experimental capacity across a range of axial force eccentricities (Fidalgo and Packer, 2024). This conservative lower bound curve can be extended to rectangular HSS, where the load interaction is checked using Eq. (5). The available moment capacity, M_available, is taken as the lesser of Eqs. (1) and (2), whereas the available tension capacity, N_available, can be determined – for the four-sided rectangular HSS end-plate connection – from the design models presented in DG24 (Packer and Olson, 2024) or the Manual Part 9 (AISC, 2023).

In Eq. (5):
P_r                 = required tensile capacity          (kips)
N_available     = available tensile capacity          (kips)
M_r                = required moment capacity      (kip-in.)
M_available     = available moment capacity     (kip-in.)

Analysis Example

A bolted end-plate connection joining two co-axial HSS 6 × 6 × 0.3125 ASTM A500 Gr. C members, as shown in Figure 4, uses a total of 8 × ¾-in. diameter ASTM F3125 Gr. A325-N (Group 120) bolts around the rectangular HSS. The end-plate is ASTM A572 Gr. 50 with a thickness of 0.625 in. Determine the connection available moment capacity, using LRFD. It is assumed the plate-to-HSS weld is designed to develop the yield capacity of the connected HSS wall.

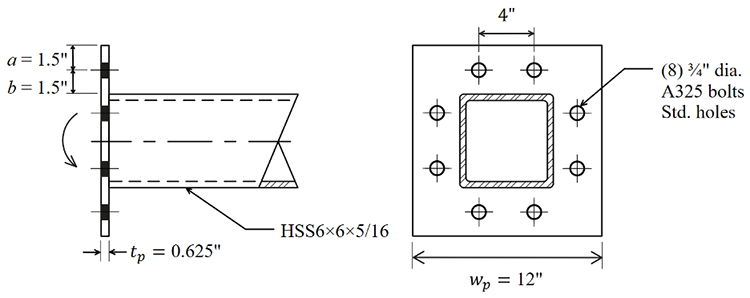
From the AISC Manual Table 2-5,           F_up = 65 ksi for the plate.
From the AISC Manual Table 1-12,         H = 6 in. and t (design thickness) = 0.291 in. for the HSS.
From the AISC Manual Table 7-2,           B_t = (φr_n/φ) = 29.8/0.75 = 39.7 kips.
d_b = 0.75 in.
a = b = 1.50 in.    a^’ = (1.50 + 0.75/2) = 1.88 in.     b^’ = (1.50 – 0.75/2) = 1.12 in.
w_p= 12 in.
n_T = 8/3 = 2.67   

• Check that the end-plate thickness is appropriate, relative to the bolt strength:

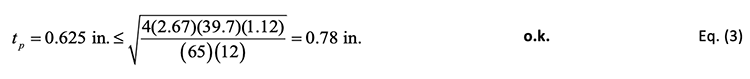
• Check that HSS meets the minimum width limit:

• Check the bolt spacing and edge distance:

Distance between bolts on adjacent sides = (2(2.5)²)^1/2 = 3.54 in. < 4 in.
Preferred min. spacing = 3d_b = 3(0.75) = 2.25 in. ≤ 3.54 in.                        o.k.        AISC Spec. Section J3.4
Min. edge distance from hole center for 3/4-in. bolt = 1 in. ≤ 1.50 in.          o.k.           AISC Spec. Table J3.4

• Available moment capacity for the limit state of bolt failure:

• Available moment capacity for the limit state of end-plate plastification:

Therefore, M_available = 543 kip-in., and the design is governed by bolt failure. Interestingly, this connection capacity is 89% of the HSS member available flexural strength, 612 kip-in. (AISC Manual Table 3-13). Since the connection design under consideration qualifies for the eight-bolt arrangement of Wheeler et al. (1998), one can calculate the connection available strength using their formulas (Key and Syam, 2014) and a value of 647 kip-in. (also governed by bolt failure) is obtained. Thus, the approach used herein is conservative.

Under axial tension loading, Chapter 7.3.2 of AISC DG24 provides a procedure for the design of rectangular HSS end-plate connections with bolts on four sides, that follows the prying design methods of the AISC Manual Part 9. A truncated version of this procedure for the analysis of a given bolted end-plate connection is presented as “Solution Method 3 – Analysis to find the tensile strength of the connecting element” in the AISC Manual Part 9. Applying this latter method to the connection example herein, the available tension capacity of the connection is calculated as N_available = 202 kips, which is 70% of the HSS member available tensile strength, 289 kips (AISC Manual Table 5-5).

As an additional exercise, check whether the connection would be acceptable under a tension force of P_r = 110 kips applied with an eccentricity of 2 in. from the HSS axis.  By substitution into Eq. (5) for combined loading, one obtains: {110/202 + 2(110)/543} = 0.95 ≤ 1.0, which is acceptable.

References

AISC. 2023. “Steel Construction Manual”, 16^th edition, American Institute of Steel Construction, Chicago, IL.

AISC. 2022. “Specification for Structural Steel Buildings”, ANSI/AISC 360–22, American Institute of Steel Construction, Chicago, IL.

ASCE. 2022. “Minimum Design Loads and Associated Criteria for Buildings and Other Structures”, ASCE/SEI 7-22, American Society of Civil Engineers, Reston, VA.

ASTM. 2025. “Standard Specification for High Strength Structural Bolts and Assemblies, Steel and Alloy Steel, Heat Treated, Inch Dimensions 120 ksi and 150 ksi Minimum Tensile Strength, and Metric Dimensions 830 MPa and 1040 MPa Minimum Tensile Strength”, F3125/F3125M–25, American Society for Testing and Materials, West Conshohocken, PA.

Fidalgo, A. and Packer, J.A. 2023. “Bolted CHS Flange-Plate Connections under Bending”, Journal of Structural Engineering, American Society of Civil Engineers, Vol. 149(6), 04023066-1 – 15.

Fidalgo, A. and Packer, J.A. 2024. “Bolted End-Plate Tube Connections Subject to Tension and Bending”, Canadian Journal of Civil Engineering, Vol. 51, pp. 73–92.

Key, P.W. and Syam, A.A. 2014. “Tubular Design Guide 24: Bolted Planar Connections”, Australian Steel Institute, Sydney, Australia.

Packer, J.A. and Olson, K. 2024. “Hollow Structural Section Connections”, Steel Design Guide No. 24, 2^nd edition, American Institute of Steel Construction, Chicago, IL.

STI. 2023. “Round HSS Bolted End-Plate Connections under Bending Moment”, Technical Article, Steel Tube Institute.

Thornton, W.A. 2017. “Yield Line Approaches for Design of End Plate Tension Connections for Square and Rectangular HSS Members using End Plate Tensile Strength”, Engineering Journal, Vol. 54, No. 3, pp. 141 – 154.

Wheeler, A.T., Clarke, M.J., Hancock, G.J. and Murray, T.M. 1998. “Design Model for Bolted Moment End Plate Connections Joining Rectangular Hollow Sections”, Journal of Structural Engineering, American Society of Civil Engineers, Vol. 124, No. 2, pp. 164 – 173.