Connecting Hollow Structural Section Members with Through-Bolts

By Jason McCormick
Associate Professor, Civil & Environmental Engineering, University of Michigan, Ann Arbor, MI, USA
July 2017

Bolting steel members is often desirable because of ease of erection and the reliability of the joint. However, direct fastening to the wall of a hollow structural section (HSS) member poses a challenge due to difficulties in accessing the inside of the member resulting from its closed shape. If the connection is near the end of the member or if the HSS is large enough for an access hole to be cut into it, then one-sided bolting (i.e. restraint provided on the outside and inside of the HSS wall through a bolt head or nut – see Figure 1(a)) can typically be accomplished to the webs or flanges of the HSS with high strength bolts (ASTM F3125 Grades A325 and A490). Alternatively, blind bolts, threaded studs, flow-drilled bolts, nails and screws are other types of mechanical fasteners that have the potential to provide a similar one-sided connection (AISC 2011). Such connections can be loaded in shear, tension, or a combination of shear and tension and design can be approached with typical bolted connection design principles (AISC 2016). If the fasteners are placed in shear, then limit states considered beyond those typically calculated for shear connections include shear bearing on the HSS wall (Packer et al. 2010). For fasteners in tension, additional limit states are needed to account for the flexibility of the HSS wall including pull-out through the wall of the HSS and HSS wall distortion (Packer et al. 2010). Often times, the controlling limit state will be dictated by the magnitude of the load and the thickness of the HSS wall.

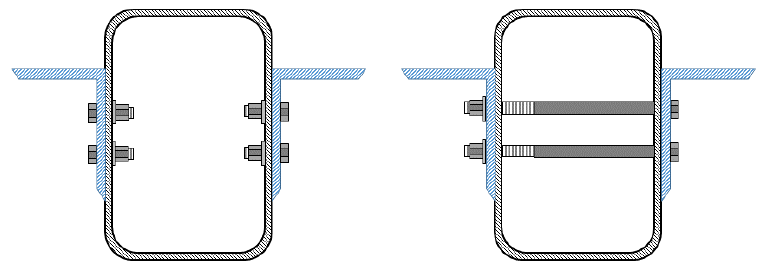
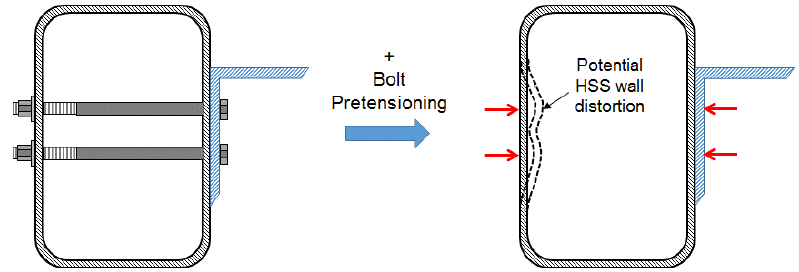
The flexibility of the HSS face combined with the fact that tensioning of the through-bolt will lead to an inward point load on the HSS face can lead to distortion of the HSS wall (Figure 2) depending on its thickness. As a result, through-bolts cannot be pretensioned in unreinforced HSS connections. The potential for this instability in the HSS wall limits the use of through-bolts to bearing connections where the bolts are only installed snug tight. Even with snug tight tensioning of the bolt (approximately 10% of the minimum bolt pretension (Table J3.1 in AISC 360-16), care must be taken when installing through-bolts with thin walled HSS so as to prevent distortion of the sidewalls. The snug tight condition by its definition (RCSC 2014) also can cause problems for through-bolting of HSS as all the plies cannot be brought into firm contact due to the void in the interior of the HSS member (Kloiber 2001). As a result, the use of through-bolts may not be practical or cost effective. However, such connections are allowed by the American Institute of Steel Construction (AISC) Specification (AISC 360-16) and are mentioned in CIDECT Design Guide 3 for Rectangular Hollow Section (RHS) Joints under Predominately Static Loading (Packer et al. 2010) and CIDECT Design Guide 9 for Structural Hollow Section Column Connections (Kurobane et al. 2004), but these connections should be well understood before they are selected for use.

Section 7 of the AISC Manual states that when a through-bolt is used to directly connect to an HSS member and the through-bolt is designed for static shear, the only limit state involving the HSS member is bolt bearing (AISC 2011). Further, Section J3.10c of the AISC Specification, which considers “Bearing and Tearout Strength at Bolt Holes”, refers the case when bolts pass fully through an unstiffened HSS member, as is the case with a through-bolt connection, to Section J7a to calculate the bearing strength as is done for a pin connection (AISC 360-16). In this case, “unstiffened HSS member” is referring to the face of the HSS that is not confined by a bolt head and nut on either side of it or stiffened by fill or reinforcement in its void (Mitchell 2012). The lack of confinement suggests that the behavior of the through-bolt more closely follows that of a pin in bearing than a bolt in bearing since the grip of the through-bolt is not restrained against expansion (Packer et al. 2010). The load distribution in a through-bolt also differs from that of a bolt or other type of mechanical fastener in a conventional bolted connection since the bolt head or nut only bears on the outside of the HSS wall and not the outside and inside as is typical of a conventional bolted connection (Rex and Easterling 2003; Duerr 2006). The bearing resistance of a pin is reduced from the bearing resistance of a bolt to account for these factors.

The limit state equation for through-bolt bearing (AISC 360-16 Equation J7-1) is given as:

R_n = 1.8F_yA_pb (θ = 0.75)
Equation (1)

R_n is the nominal bearing strength of the HSS member per through-bolt, F_y is the specified minimum yield strength of the HSS wall, and A_pb is the projected area in bearing. Based on Equation 7-15 in the AISC Manual (AISC 2011), the projected area in bearing is a function of the diameter of the through-bolt, d, and the design wall thickness of the HSS, t_design (0.93t for ASTM A500 or t for ASTM A1085). Thus, the projected bearing area for a single through-bolt can be calculated as:

A_pb = dt_design
Equation (2)

Equation 1 (AISC 360-16 Equation J7-1) is used to calculate the bearing strength of the HSS wall per through-bolt where the total bearing strength of the HSS wall can be obtained by summing over the number of through-bolts present in the connection. The nominal bearing strength of the member connected to the HSS also needs to be checked using the same equation as a result of the lack of restraint against through-bolt grip expansion. As with other bearing joints, bolt shear strength (AISC 360-16 Equation J3-1) and all other limit states associated with the connected member need to be calculated in order to complete the analysis or design of the connection. It should further be noted that the AISC Specification (AISC 360-16) does not explicitly address tear-out for through-bolted connections. However for connections where through-bolts are closely spaced together parallel to the direction of loading or are located close to the end of the member, it may be necessary for the engineer to develop a rational approach to considering this limit state keeping in mind the lack of confinement provided by the through-bolt.

Considering other design approaches for through-bolts, Eurocode (EN 1993 1-8:2010) does not specify a specific procedure for analyzing these connections. Assuming a similar approach to AISC is taken whereby the pin bearing strength is used to calculate the bearing strength of a through-bolt instead of bolt bearing strength, the bearing resistance can be calculated as:

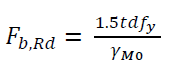
Where F_b,Rd is the design requirement for bearing resistance of the plate and pin, t is the thickness of the connected part, d is the diameter of the pin, ƒ_y is the lower of the design strengths of the pin and the connected part, and γ _M0 is the partial safety factor for calculating the resistance of members and cross-sections. The 1.5 factor in Equation 3 suggests a slightly more conservative value compared with AISC 360-16 (Equation 1).

Unlike AISC which leaves calculation of the bending resistance of the pin up to the engineering judgement, Eurocode 3 (EN 1993 1-8:2010) specifies a means of calculating the bending resistance of the pin:

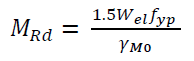
M_Rd is the design requirement for bending resistance of the pin, W_el is elastic section modulus of the pin, and ƒ_yp is the yield strength of the pin. An interaction equation can then be used to account for combined shear and bending resistance of the pin. One thing to note in considering Eurocode’s approach to pin connections is that if no significant rotation of the pin is required and the length of the pin is less than 3 times its diameter, then the pin connection can be designed as a single bolted connection. However, most through-bolt connections probably will not meet this maximum length requirement as it significantly limits the size of the HSS member.

The above requirements all refer to the case where the HSS member is unstiffened. In this situation, it becomes clear that a through-bolt connection is often not practical due to the inability to pretension the bolt leading to a required reduction of the bearing strength (i.e. the use of the bearing resistance of a pin). One of the most common methods for improving the performance of through-bolt connections is to provide a sleeve (or round tube) for the through bolt to pass through (Figure 3). The sleeve is achieved by drilling a hole in the HSS, inserting a sleeve that has an inner diameter equal to the diameter of a standard hole for the through-bolt, and then welding the sleeve in place (Dutta et al. 1998). The sleeve allows pretensioning of the bolt while preventing distortion of the HSS wall. As a result, the through bolted connection will behave more like a bolted joint rather than a pin joint. However, the cost of such a connection should be considered along with the number of alternative means (access holes, blind bolts, threaded studs, flow-drilled bolts, nails, and screws) of providing a single sided connection to HSS that may be more practical.

References

AISC. (2011). “Steel Construction Manual, 14th edition”. American Institute of Steel Construction, Chicago, IL.

AISC. (2016). “Specifications for Structural Steel Buildings”. ANSI/AISC 360-16. American Institute of Steel Construction, Chicago, IL.

Duerr, D. (2006). “Pinned Connection Strength and Behavior”. ASCE Journal of Structural Engineering, 132(2), 182-194.

Dutta, D., Wardenier, J., Yeomans, N., Sakae, K., Bucak, O. and Packer, J.A. (1998). Design Guide 7: For Fabrication, Assembly and Erection of Hollow Section Structures. CIDECT, Germany.

EN (2010). “Eurocode 3: Design of Steel Structures – Part 1-8: Design of joints”. EN 1993-1-8:2010. European, Committee for Standardization, Brussels, Belgium.

Kloiber, L. (2001). “Designing HSS Connections”. Modern Steel Construction, November 2001.

Kurobane, Y., Packer, J.A., Wardenier, J., and Yeomans, N. (2004). Design Guide 9: For Structural Hollow Section Column Sections. CIDECT, Germany.

Mitchell, H. (2012). “Steel Interchange: Bearing Strength at Bolt Holes in HSS”. Modern Steel Construction, December 2012.

Packer, J., Sherman, D., and Lecce, M. (2010). “Steel Design Guide 24: Hollow Structural Section Connections”. American Institute of Steel Construction, Chicago, IL.

Packer, J.A., Wardenier, J., Zhao, X.-L., van der Vegte, G.J. and Kurobane, Y. (2010). Design Guide 3: For Rectangular Hollow Section (RHS) Joints under Predominantly Static Loading 2nd Edition. CIDECT, Canada.

Related Resources

• Webinar On Demand: Through-Bolts and Blind Bolts to HSS
• Bolting to HSS Members
• HSS Blind Structural Fasteners