Round Branch-to-Rectangular Chord HSS Connections
Bahen/Tanenbaum Professor of Civil Engineering, University of Toronto, Ontario, Canada
AISC 360 gives design procedures for round branch-to-round chord HSS welded connections, and for rectangular branch-to-rectangular chord HSS welded connections (where rectangular includes square). These limit state checks are contained in Chapter K of the current Specification (AISC, 2010), in Chapters J and K in the forthcoming edition of the Specification (AISC, 2016), and in AISC Design Guide No. 24 (Packer et al., 2010). However hybrid trusses, which are not covered by AISC design guidance, involving a mix of round and rectangular HSS members, do occasionally occur. Pipe sections may potentially be readily sourced, and used for branch members, yet square or rectangular HSS might be preferred for the chords to make fabrication easier. As shown in Figure 1(a), only straight cuts to the round branches are required for gapped K-connections. For overlapped K-connections, however, some tube profiling will be required for the overlapping round HSS branch member (Figure 1(b)); the overlapped round branch would be straight cut and welded directly to the flat chord face. Hybrid trusses using square or rectangular branches welded to round HSS (or pipe) chord members would be very impractical, because of the profiling required for all branch member ends.
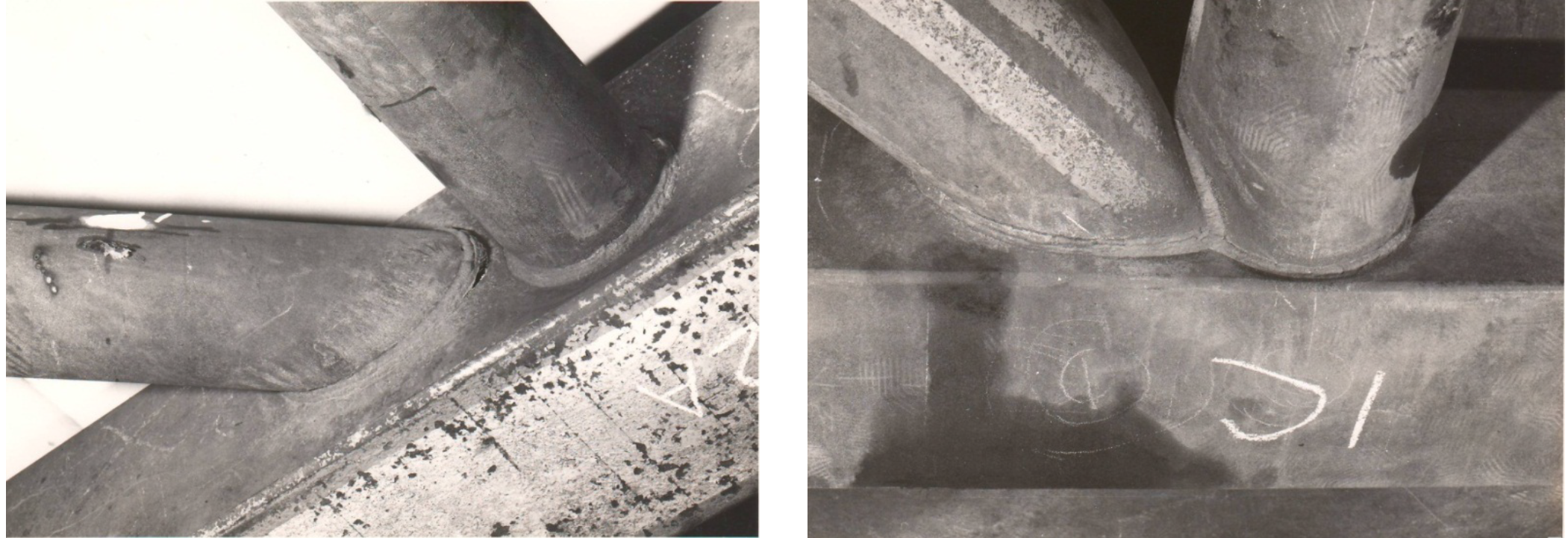
Left image: gapped K-connection
Right image: overlapped K-connection
Experimental research has been performed on a considerable number of round-to-rectangular HSS N-connections (a special case of the general K-connection) and it has been observed that the connection limit states resemble those of similar rectangular HSS connections. An inspection of contemporary design recommendations reveals that most failure modes for hollow section connections are dependent on the circumference or “footprint” of the branch member at the joint with the chord, or dependent on the cross-sectional area of the branch members. The perimeter of a round HSS of diameter Db is πDb, and that of a square HSS of width Db is 4Db (excluding the rounded corners), thus approximately in the ratio of π : 4. Similarly, the cross-sectional area of a thin round HSS of diameter Db and thickness tb is approximately πDb tb, whereas the cross-sectional area of a thin square HSS of width Db and thickness tb is approximately 4Db tb, again in the ratio of π : 4. (Note that well-designed HSS trusstype connections will have branches that are thin relative to the chord thickness). It was hence surmised 2 that round-to-rectangular HSS welded connections could potentially be treated as square-to-rectangular HSS connections, by converting the round branch members to square sections.
Branch Conversion Method
This method has been examined by analyzing the results of 40 gapped and overlapped round-to square HSS N-connections (as shown in Figure 1), tested as both isolated connections and as connections within complete trusses, of which 27 tests resulted in connection failure (Packer et al., 2007). Implementation of this method involves replacing round branches (of diameter Db) by square branches of width πDb/4, keeping the amount of gap or overlap the same and the thickness the same, and then using rectangular HSS connection design formulas. Alternatively, since the conversion is approximate anyway, one might perhaps just assume the round branch to be a square of width Db, calculate the connection resistance using rectangular HSS design formulas, and then multiply this connection capacity by π/4. Either implementation produces the same result for gapped K- and Nconnections, but a different result for overlapped K- and N-connections. Correlation with experimental results showed that the branch conversion process was valid, for both gapped and overlapped connections, with very little difference evident between the two interpretation methods for overlapped connections (Packer et al., 2007). Recent international design recommendations for HSS connections (Packer et al., 2009; ISO, 2013) have followed the simpler route of assuming each round branch to be a square of width Db, calculating the connection resistance using rectangular HSS design formulas, and then multiplying this connection capacity by π/4. Moreover, the principle has been extended to axially loaded round-to-rectangular HSS T-, Y- and X- (cross) connections.
Application to AISC 360-10
In Table K2.2: Available Strengths of Rectangular HSS-to-HSS Truss Connections, round HSS branches with 0.25 ≤ Db/B ≤ 0.80 can be accommodated by the following:
- For T-, Y- and Cross Connections, replace both Bb and Hb by Db in the following equations and in participating variables: (K2-7), (K2-8), (K2-12) and (K2-13); then multiply the resulting connection available strength by π/4. No reduction by π/4 is required for the chord shear criterion (in the rare instances where this limit state applies). The Limits of Applicability are generally those in Table K2.2A but round branches are also subject to the Db/tb limits in Table K2.1A.
- For Gapped K-Connections, replace both Bb and Hb by Db in the following equations and in participating variables: (K2-14), (K2-15), (K2-16) and (K2-13); then multiply the resulting connection available strength by π/4. No reduction by π/4 is required for the chord shear criterion. The Limits of Applicability are generally those in Table K2.2A, but round branches are also subject to the Db/tb limits in Table K2.1A and Db/B ≥ 0.1 + γ/50.
- For Overlapped K-Connections, replace both Bbi and Hbi by Dbi, plus Bbj by Dbj, in the following equations: (K2-17), (K2-18), (K2-19), (K2-20) and (K2-21); then multiply the resulting connection available strength by π/4. Equation (K2-22) requires no modification. The Limits of Applicability are generally those in Table K2.2A but round branches are also subject to the Db/tb limits in Table K2.1A.
References
AISC. 2010. “Specification for Structural Steel Buildings”, ANSI/AISC 360-10, American Institute of Steel Construction, Chicago, IL, USA.
AISC. 2016. “Specification for Structural Steel Buildings”, ANSI/AISC 360-16, American Institute of Steel Construction, Chicago, IL, USA.
ISO. 2013. “Static Design Procedure for Welded Hollow-Section Joints – Recommendations”, ISO 14346:2013(E), International Standards Organisation, Geneva, Switzerland.
Packer, J.A., Mashiri, F.R., Zhao, X.L. and Willibald, S. 2007. “Static and Fatigue Design of CHS-to-RHS Welded Connections using a Branch Conversion Method”, Journal of Constructional Steel Research, Vol. 63, pp. 82-95.
Packer, J.A., Sherman, D. and Lecce, M. 2010. “Hollow Structural Section Connections”, Steel Design Guide No. 24, American Institute of Steel Construction, Chicago, IL, USA.
Packer, J. A., Wardenier, J., Zhao, X.-L., van der Vegte, G.J. and Kurobane, Y. 2009. “Design Guide for Rectangular Hollow Section (RHS) Joints under Predominantly Static Loading”, CIDECT Design Guide No. 3, 2nd edition, Comité International pour le Développement et l’Étude de la Construction Tubulaire, Geneva, Switzerland, ISBN 978-3-938817-04-9.
January 2016