Rectangular HSS Connections Close to a Chord End
By Jeffrey A. Packer
Bahen/Tanenbaum Professor of Civil Engineering, University of Toronto, Ontario, Canada
Research into the behavior of truss-type, welded HSS connections in the last 50 years has resulted in connection design guidelines published in North America (Packer and Henderson 1997; AISC 2005, 2010; Packer et al., 2010 ) and internationally (CEN 2005, Packer et al. 2009, ISO 2013). All of these HSS design recommendations, either by explicit statement or by implication from the illustrations, assume that the chord member has ample continuity beyond the connection region. Up until 2016, there has been no established guidance for the case when an HSS branch member is near an open end of an HSS chord member in a girder or truss (Figure 1). Designers were restricted to capping the chord with an end plate, reinforcing the chord walls, or using “engineering judgment”, for this recurring practical problem. However, there should be a minimum end distance, lmin, from an open chord end at which full connection capacity can be achieved for an unreinforced connection.

Analytical Models
Yield line analysis has long been used to estimate the capacity of flexible connections between rectangular HSS. When a connection is remote from the HSS chord ends (termed a “regular” connection), the analytical solution for the yield load Pn [Equation (1)], associated with the chord plastification limit state, can be derived based on a symmetric flexural yield line mechanism developing in the chord connecting face, such as the rectilinear pattern of Figure 2(b). Equation (1) has been widely adopted in design recommendations for rectangular HSS-to-HSS T-, Y-, and Cross- (or X-) connections, and is Equation (K2-7) in AISC 360-10. In this equation, sinθ allows for an inclined branch at θ < 90o, Fy is the chord yield stress, t is the chord wall design thickness, β is the branch-to-chord width ratio = Bb/B (see Figure 2), η is a load-length parameter = Hb/Bsinθ (see Figure 2), and Qf is a strength reduction factor (≤ 1.0) to account for the effect of normal stress in the chord connecting face.
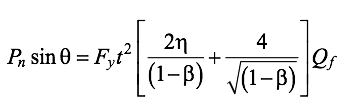
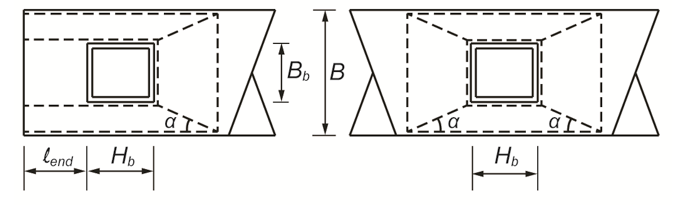
Left image: (a) HSS branch near an open chord end
Right image: (b) HSS branch remote from the chord ends
If β approaches unity, Pn tends to infinity and this limit state is not likely to be critical. β ≤ 0.85 thus represents a practical upper limit for the application of the yield line solution. The explicit solution of Equation (1) is not given in the latest AISC Specification (AISC 2016) Chapter K, and instead has to be calculated from Section J10.10 of Chapter J, with the help of Part 9 of the AISC (2017) Manual.
When a connection is near an HSS chord end (termed an “end” connection), there may not be adequate lengths to develop the traditional yield line mechanism of Figure 2(b). A potential asymmetric flexural yield line mechanism [Figure 2(a)] has therefore been proposed and investigated for its ability to predict the yield load of such end connections, for a given end distance lend from the branch edge to the open chord end. The solution for this yield-line mechanism is given by:
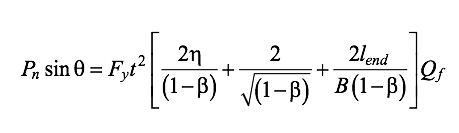
It can be shown that the regular yield line mechanism [Figure 2(b) and Equation (1)] controls and predicts a lower yield load compared to the end connection yield line mechanism [Figure 2(a) and Equation (2)] only if the end distance is such that:
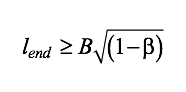
The inequality or “Equation” (3) is now included as a limit of applicability for Equation (1) in the latest AISC Specification (AISC 2016) Table K3.2A for T- and Y-connections. However, note that it would also be applicable to Cross-connections. Since Equation (3) is derived from a comparison of yield-line solutions, it can only be expected to be valid in the parameter range for which yield-line mechanisms are appropriate (i.e. when β ≤ 0.85). This end-distance requirement could moreover also be applied to an axially loaded longitudinal plate branch-to-HSS connection, by considering the plate as a rectangular HSS of dimensions Hb x Bb. If an HSS branch or longitudinal plate branch is close to a chord open end and the end distance does not satisfy Equation (3) then, as an alternative to taking the reduced connection nominal strength associated with Equation (2), the chord end is often capped and a connection strength given by Equation (1), or higher, is assumed to be achieved. There is, therefore, no minimum end distance requirement in the case of a chord-end cap plate.
Validation
Twelve HSS-to-HSS connections have been fabricated and tested in the laboratory under quasi-static branch axial loading, as illustrated in Figure 3, to assess the foregoing theory. Two ASTM chord sizes (HSS 8”x8”x1/4” and HSS 8”x8”x3/8”) and one branch size (HSS 4”x4”x3/8”) were selected, enabling one nominal β ratio of 0.5 and two nominal B/t values of 32 and 21. Although having the appearance of a T-connection, each test specimen would be classified as a Cross-connection because the branch compression load is transferred through the chord to the opposite side [see AISC 360-16 Commentary on Section K1 and AISC Design Guide No. 24 (Packer et al., 2010)]. The end distance, lend, from the open chord end was varied parametrically until a “regular” connection with the branch remote from the end was attained, as a “control” specimen. Using carefully measured geometric and mechanical properties of the test specimens, the connection yield loads were very well-predicted by taking the lower of the loads given by Equations (1) and (2). The connection yield loads were determined experimentally from the branch load versus chord face deformation plots, using a deformation limit proposed originally by Lu et al. (1994) and now advocated by the International Institute of Welding (IIW). Despite being theoretical upper bounds these Equations (1) and (2) are still conservative, as experimental yield loads always exceeded the predicted yield loads (with the mean of the actual-to-predicted ratio being 1.29 and having an associated coefficient of variation (COV) of only 5.3%).


Capping of the Chord End
Welding a cap plate to the chord end, for two test specimens with a low lend value (see Figure 4), was found to restrain chord deformation and stiffen the connection, such that the connection yield loads exceeded those of the control specimens (with branches remote from the chord end). Chord capping is thus an effective means of developing the full connection strength, provided the cap plate is welded all-around as was done for the test specimens. Since AISC 360-16 does not provide Equation (2), where a short end distance occurs () and end-capping of the chord is not done the AISC 360-16 Commentary advocates reducing the regular full connection strength by 50%, in lieu of detailed calculations [such as by Equation (2)]. The experimental results have also shown that taking 50% of the nominal strength per Equation (1) is safe for design in such end-cap situations.
Application to Design
Since Equations (1) and (2) are deformation-controlling limit states, and they predict connection yield loads that are far below the ultimate capacity, the available connection axial strength for design for each can be calculated by multiplying by φ = 1.0 (for LRFD) or by dividing by Ω = 1.50 (for ASD). A rectangular HSS-to-HSS gapped or overlapped K-connection, designed in accordance with AISC 360-16 Tables K3.2 and K3.2A, produces a less-flexible connection than its Y-connection counterpart, so the application of the end-distance rule given in Equation (3) for T-, Y- and Cross-connections should be conservative for un-capped rectangular HSS K- (and N-) connections.
Strain gauge instrumentation on the branches of test specimens, located close to the connecting fillet weld has, as expected, confirmed a highly non-uniform loading around the branch perimeter and hence the adjoining weld. It has been found that the weld effective length recommended for a regular T-, Y- and Cross-connection, which is used to proportion the weld for the actual axial force in the branch, can also be adapted to an un-capped end connection with a slight modification. The weld effective length, le, given in Equation (K5-5) of AISC 360-16 Table K5.1, can be modified to:
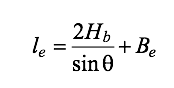
where Be is given by Equation (K1-1) of AISC 360-16. Equation (4) reflects the further-reduced effectiveness of the transverse weld near an open chord end.
References
AISC. 2005. “Specification for Structural Steel Buildings”, ANSI/AISC 360-05, American Institute of Steel Construction, Chicago, IL.
AISC. 2010. “Specification for Structural Steel Buildings”, ANSI/AISC 360-10, American Institute of Steel Construction, Chicago, IL.
AISC. 2016. “Specification for Structural Steel Buildings”, ANSI/AISC 360-16, American Institute of Steel Construction, Chicago, IL.
AISC. 2017. “Steel Construction Manual”, 15th Edition, American Institute of Steel Construction, Chicago, IL.
CEN. 2005. “Eurocode 3: Design of Steel Structures – Part 1-8: Design of Joints”, EN 1993-1-8, European Committee for Standardization, Brussels, Belgium.
ISO. 2013. “Static Design Procedure for Welded Hollow-Section Joints – Recommendations”, ISO 14346, International Organization for Standardization, Geneva, Switzerland.
Lu, L.H., de Winkel, G.D., Yu, Y. and Wardenier, J. 1994. “Deformation Limit for the Ultimate Strength of Hollow Section Joints”, Proceedings of the 6th International Symposium on Tubular Structures, Melbourne, Australia.
Packer, J.A. and Henderson, J.E. 1997. “Hollow Structural Section Connections and Trusses – A Design Guide”, 2nd edition, Canadian Institute of Steel Construction, Toronto, ON.
Packer, J.A., Sherman, D. and Lecce, M. 2010. “Hollow Structural Section Connections”, Steel Design Guide No. 24, American Institute of Steel Construction, Chicago, IL.
Packer, J.A., Wardenier, J., Zhao, X.-L., van der Vegte, G.J. and Kurobane, Y. 2009. “Design Guide for Rectangular Hollow Section (RHS) Joints under Predominantly Static Loading”, CIDECT Design Guide No. 3, 2nd edition, Comité International pour le Développement et l’Étude de la Construction Tubulaire, Geneva, Switzerland.
May 2017