HSS-to-HSS Connections
By Kim Olson, PE
Technical Consultant, Steel Tube Institute
In truss design, minimum weight of the truss does not equal least cost. Fabrication costs factor heavily into the cost of the finished structure. A truss that has fewer connections and members may be less expensive, even though it would require larger and/or thicker chord and branch (or web) members. The selection of HSS members for trusses is not as simple as choosing the lightest available shapes. Due to the flexibility of their walls, local strength of an HSS at the connection may control the capacity of the connection. Understanding this while sizing members will mean efficient and economical connections without the need for costly stiffeners or reinforcing. Even if the Engineer of Record (EOR) is not doing the final connection design, some member checks should be performed to ensure proper joint strength. The joint strength is determined by member sizes and geometry, which are directly under the EOR’s control.
In order to optimize HSS connections, certain rules of thumb should be kept in mind. It is generally beneficial to select thicker chord members. The diameter-to-thickness ratio (for round shapes) or face width-to-thickness ratio (for square/rectangular shapes) should range from 15 to 30. Branch members are best when they’re relatively thin (keep the ratio of the branch thickness to chord thickness low), but keep the width ratio (width of the branch to width of the chord) high. Another thing to consider is that when the chord and branch members are the same width, the weld of the sidewalls can be difficult to make. For larger members this could require profiling of the sidewall of the branch to contour to the radius of the chord, using backing that cannot be removed, or placing a weld bead on the corner of the chord member that acts as a backing.
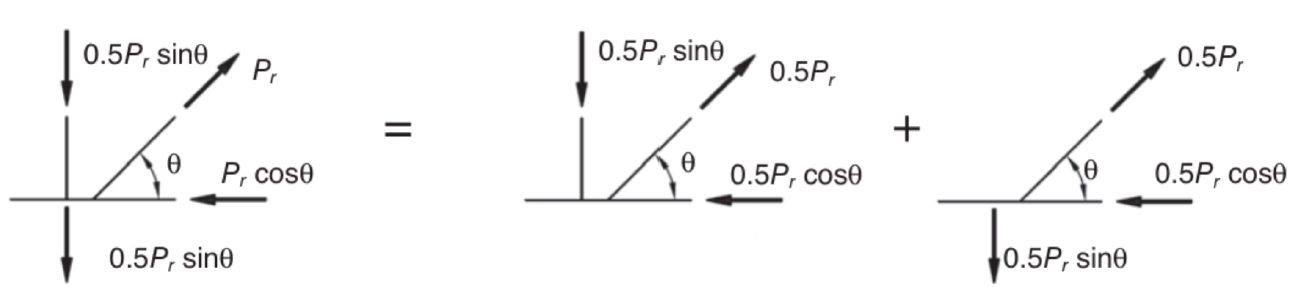
When designing truss connections, it is important to know which type of connection is present. There are three types of truss connections—K (includes N connections), Y (includes T connections), and X (or cross). The type is based on the method of force transfer in the connection and not on the physical appearance of the connection. In a K connection, the punching load from one branch member is essentially equilibrated (within 20%) by other branch members (Figure 1a and 1b). In a Y connection, the punching load is equilibrated by beam shear in the chord member (Figure 1d). In X/cross connections, loads are transferred through the chord member and equilibrated on the other side of the chord. This force could be resisted by a brace; it does not have to be resisted by other branch members (Figure 1e, 1g and 1h). If branch members transmit part of their load as K connections and part as Y or X connections, the adequacy of the connections shall be determined by interpolation on the proportion of the available strength of each in total (Figure 1c and 2).
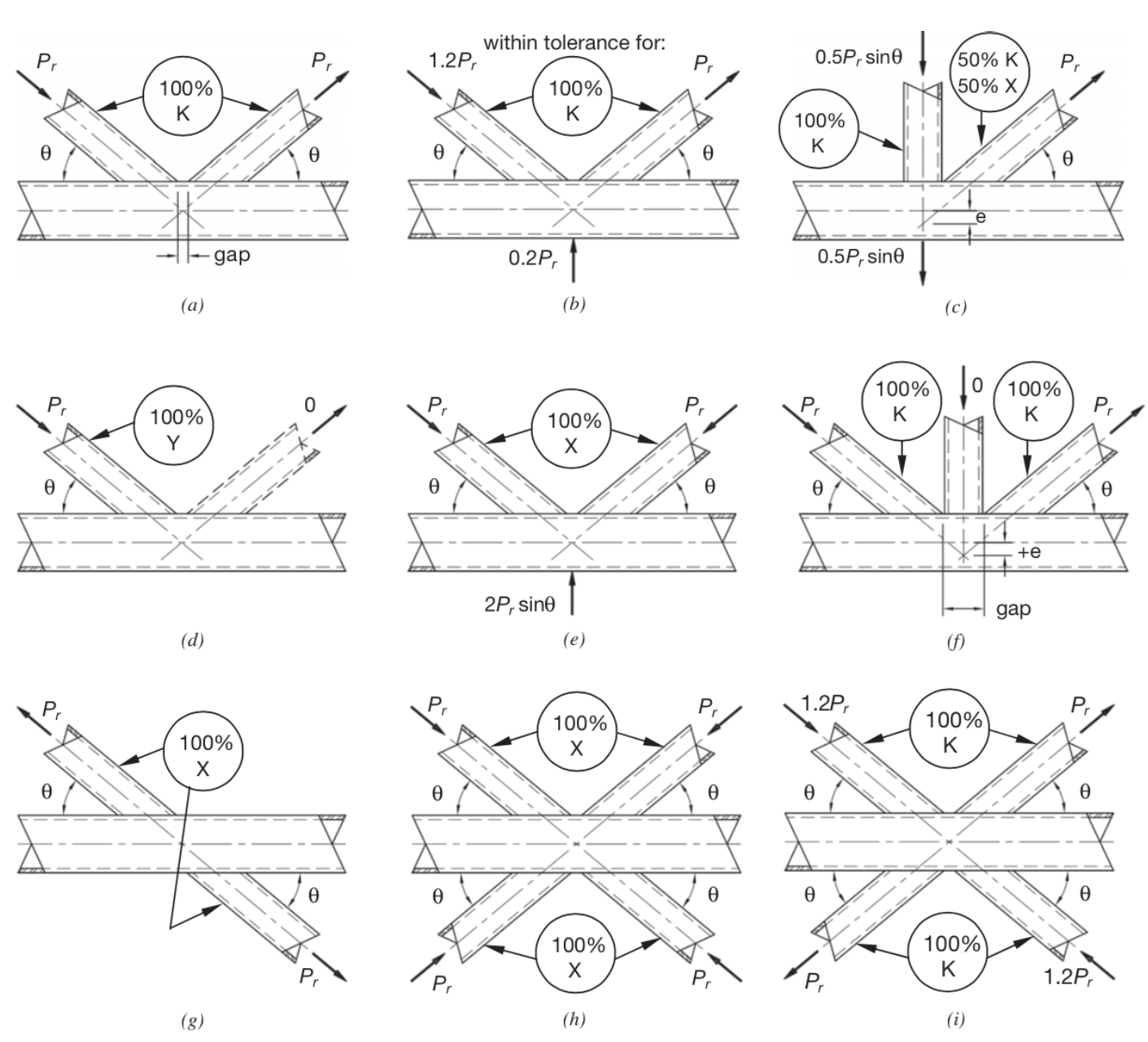
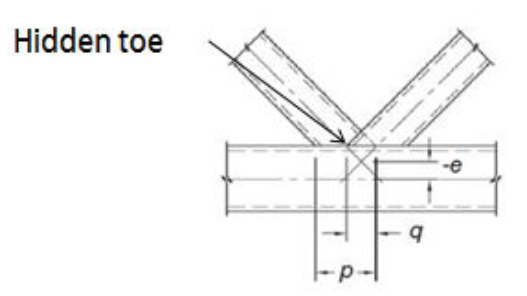
K connections can be classified as gapped or overlapped. In a gapped K connection, there is a gap on the chord face between the faces of the two connecting branch members. If the gap size becomes large enough, the K connection should be treated as two separate Y connections. In an overlapped K connection, one branch member connects partially to the chord face and partially to the other branch member. Both types have their advantages—overlapped connections lead to a stronger joint and a stiffer truss, and gapped connections are less expensive and much more feasible when using round members. In overlapped K connections, it is important to consider whether it is required to weld the “hidden toe” of the overlapped member (Figure 5). When there is 100% overlap of the two branch members, it is very important to weld the hidden toe. If the members are partially overlapped, it may be possible to avoid welding the hidden toe. If the force components normal to the chord differ by 20% or less and the remaining welds to the overlapped branch develop the full capacity of the branch member walls, welding of the hidden toe is not required. If the normal forces differ by more than 20%, the more heavily loaded member should be the overlapped member and its perimeter fully welded. It is important to consider this early on, as many fabricators prefer to tack weld both branches and then fully weld them—this can’t be done if the hidden toe needs to be welded.
Equations for checking truss connections are shown in AISC 360-10, tables K1.1, K1.2, K2.1, and K2.2. At the end of each table are limits of applicability for the equations. These limits represent both fabrication feasibility and the range of parameters over which the equations have been verified in experiments. These limits of applicability also consider some eccentricity—if they are satisfied, secondary moments in the connections do not need to be considered.
When sizing a weld for applied forces, an effective weld length must be used instead of an actual length. Due to the variation of flexural stiffness of the HSS wall across the section width, the force transmitted through the weld is not uniform. The load is highest at the ends closest to the sidewalls and smallest in the middle. To account for this, a reduced effective weld length is used in calculations. Proper joint sizing should result in a fillet weld whenever possible.
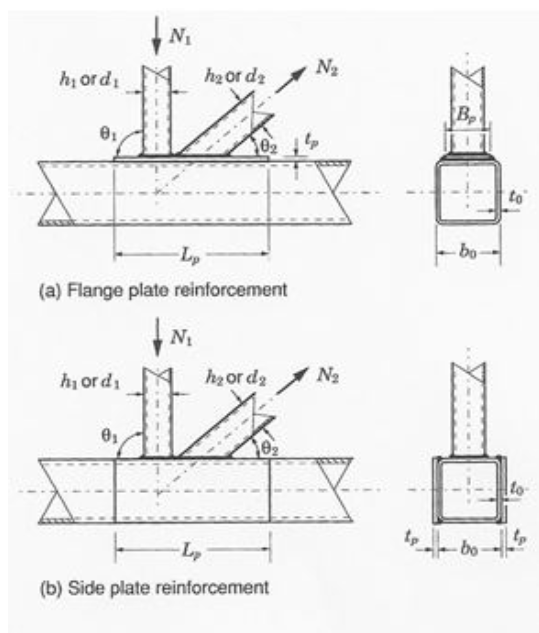
It is possible to stiffen truss connections with added plates. If chord plastification is controlling, a flange plate can be added to the connecting face of the chord (Figure 6a). If the chord is overstressed in shear, side plates can be added to both sides of the chord member (Figure 6b). It is also possible to fill a critical length of the chord with concrete or grout. These options involve added material and labor and are therefore likely more expensive than selecting a stronger chord shape from the beginning, but they are options if it is discovered that a chord needs to be enhanced.
November 2014