HSS Limit States in Cap Plate Connections
By Cathleen Jacinto, PE, SE
FORSE Consulting, Technical Consultant to the Steel Tube Institute
Introduction
A commonly used hollow structural section (HSS) connection type consists of ‘line loads’ applied to the end of an HSS member via a cap plate, or via the flange of a WT. One example of this connection type is a wide flange (WF) beam framing over an HSS column, in which the bottom flange of the WF beam is bolted to a cap plate which is welded to the top of an HSS column (Figure 1). In this case, WF beam shear reactions are imparted onto the HSS column below in local bearing. There may also be a moment transferred across the beam-to-column interface, resulting in tension and compression forces applied to the end of the capped HSS column. Alternately, a WT (or cap plate with a transverse stem plate) can be welded to the top of an HSS member to transfer concentrated loads (Figure 3).
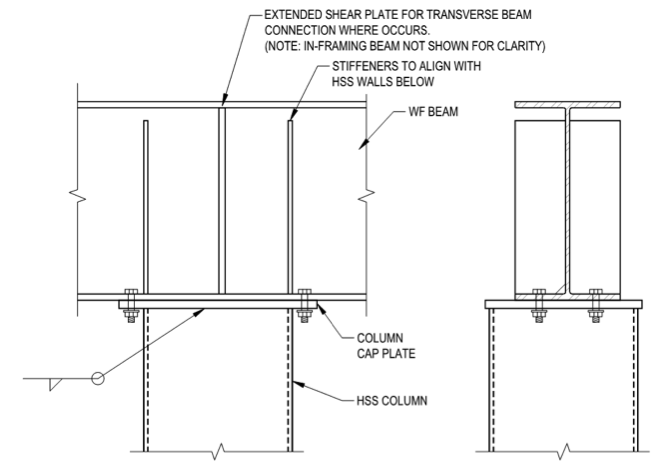
There are several limit states required to be checked to confirm the adequacy of the cap plate, beam or WT, and the HSS column, but this article will focus on reviewing limit states specific to the HSS section. When a tension or compression force is applied to the end of a capped HSS axial member across nearly its full width, failure of the HSS walls is possible. Local yielding and local crippling of round or rectangular (including square) HSS sidewalls are potential limit states to consider. We will explore how to apply AISC 360 Specification Chapter J10 requirements to HSS wall limit state checks for HSS cap plate connections.
Shear Lag Design Considerations
When a tensile or compressive force is transferred from a transverse web or plate to a cap plate, this force is dispersed over a width across the round or rectangular HSS walls below. This width is directly dependent on the thickness of the transverse web or plate and the thickness of the cap plate. A very thick cap plate will distribute this concentrated load more uniformly and across a larger width, activating more of the walls of the HSS column than a very thin cap plate. This is the shear lag effect; the potential for uneven stress distribution that results when the HSS cross section is not uniformly and fully loaded. The design method for checking the HSS walls in cap plate connections recognizes that shear lag will be present in the HSS if portions of the cross-section are not loaded.
To understand how shear lag is considered in cap plate connections, we explore the load path through the connection elements. Per AISC 360 Specification, Section J10.2 Commentary for Local Yielding, a concentrated load from the transverse web or plate is spread over a stress zone with a slope of 2.5:1 in local yielding. This stress zone starts at the top of the cap plate and extends through the plate to the HSS walls below. Figure 2 illustrates the transverse web bearing width, B, oriented for load dispersion into the HSS wall of width, lb. This can also be applied to the diameter, D, of a round HSS. The distribution slope relative to local yielding of 2.5:1 from each face of the transverse web produces a dispersed load width of (5tp + lb).
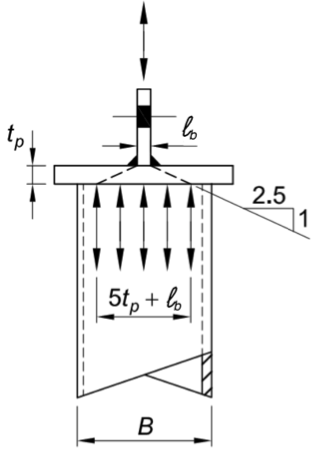
AISC 360-16 Fig. C-K2.2
Load dispersion from a concentrated force through a cap plate
If (5tp + lb) is less than B, then only two HSS walls are engaged to resist the single concentrated load applied from the transverse web. And for these two effective walls, only a partial width of (5tp + lb) can be considered to resist the applied load. Note, however, that if a moment is applied to the cap plate, then only two HSS walls are available to resist the moment force couple. In this case, one HSS wall resists the tension force and a second HSS wall resists the compressive force.
If (5tp + lb) is greater than B, then the full HSS section is effective in resisting the load. All four walls in a rectangular HSS walls or the full gross area of a round HSS can be considered. In this case, no shear lag is present. This is obviously the most efficient condition for resisting load in the HSS, but may require a very thick plate in order to accomplish this.
The next section will clarify how to more specifically apply shear lag considerations in checking the HSS section for local yielding and local crippling.
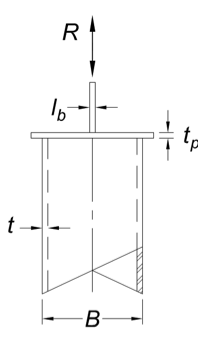
HSS Column Cap Plate Connections – Limit State of Wall Local Yielding
When a concentrated tensile or compressive force acts on the end of a round or rectangular HSS column with a cap plate, and the force is in the direction of the HSS axis, the walls of the HSS member could fail in sidewall yielding, with consideration of shear lag. The concentrated force may be due to local bearing or a moment connection.
The nominal strength in local yielding of round or rectangular HSS walls to resist tension or compression load can be determined by AISC 360 Specification Eq. (J10-2). In yielding, the load is assumed to distribute from the top of cap plate down at a slope of 2.5:1, resulting in a dispersed load width of (5tp + lb).
Below is a summary of variables to assume in Specification Eq. (J10-2):
Fyw=Fy of HSS Column
k=Cap plate thickness, tp
tw=HSS wall thickness, tdes
lb=Transverse Plate or Web Thickness
d=B/2
Qf is omitted
Incorporating these variables into AISC 360-16 Specification Eq. (J10-2) results in the nominal strength in HSS wall local yielding, for one wall:
Rn = FyHSS tdes (5tp+lb )
Equation (1)
Φ = 1.00,Ω = 1.50
As discussed above, if (5tp + lb) < B, then only two HSS walls are effective due to shear lag. Therefore, the yielding nominal strength to resist a concentrated load, for two walls:
For (5tp+lb ) < B for rectangular HSS (or < D for round HSS):
Rn = 2FyHSStdes(5tp+lb ) ≤ FyHSSAg
Equation (2)
It should be noted that if the tensile or compressive force is due to an applied moment onto the cap plate, then only two HSS walls are available to resist the moment. Therefore, only one wall is effective in resisting the tensile force couple and one wall to resist compression. In this instance, the nominal strength for one wall per Eq. (1) should be used to resist each of the tension or compression coupled force.
If (5tp + lb) > B, then shear lag is not present, and the full HSS section is effective in resisting the concentrated load. Therefore, the nominal local yielding strength, for all HSS walls:
For (5tp+lb ) > B for rectangular HSS (or > D for round HSS):
Rn = FyHSSAg
Equation (3)
AISC 360-16 Specification Eq. (J10-2) applies to connection forces located greater than member depth, d, from the member end. This is analogous to wide-flange beams bearing on a seated connection, and the full (5k + lb) width cannot disperse on both sides of the bearing plate at the beam end. In our connection condition, if the transverse web or plate is centered upon the HSS cap plate, then the full dispersed (5k + lb) width can be achieved and Eq. (J10-2) can be used. However, if the transverse web is eccentric to the HSS column centerline and/or the full dispersed (5k + lb) width per Figure 2 cannot be achieved, then it would be more appropriate to base the local yielding limit state check on Eq. (J10-3).
HSS Column Cap Plate Connections – Limit State of Wall Local Crippling
HSS Column Subject to Axial Compression
This limit state applies to the walls of a square or rectangular HSS member subject to a concentrated compressive force. The force is applied in the direction of the HSS axis, acting on the end of the HSS member via a cap plate. The concentrated load may be due to local bearing or a moment connection.
The capacity of the HSS sidewalls to resist crippling can be determined using AISC 360-16 Specification Eq. (J10-4). This equation assumes the compressive force is applied at a distance from the member end that is greater than or equal to d/2, while Eqs. (J10-5a) and (J10-5b) apply to forces at a distance to member end less than d/2. The Commentary for Section J10.3 clarifies that Eqs. (J10-5a) and (J10-5b) are intended for beam ends where the web is unsupported, such as at seated connections. Although our connection condition occurs at the end of the HSS member, the HSS walls are considered supported by the cap plate, and Eq. (J10-4) is applicable.
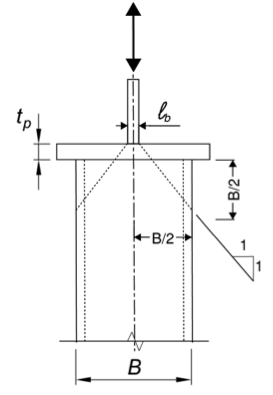
Similar to local yielding of the walls, the compression load is assumed to disperse from the base of the transverse web or plate through the cap plate over a specific width of the HSS walls. For buckling, a distribution slope can be assumed as 1:1 from each face of the transverse web. This is based upon a model in which the force is assumed to spread out at a 45 degree angle in both directions from the point of load for buckling and crippling, as shown in Figure 4. Therefore, the force will distribute across the full HSS width, B, and at a depth no greater than B/2. In terms of wide flange connections, the web local crippling phenomenon has been observed to occur in the wide flange web adjacent to the loaded flange. In our case, crippling would occur in the affected HSS wall(s) adjacent to the cap plate within a depth of B/2. Therefore, the web (or wall) depth is taken as half of the full width of the HSS, or B/2.
The coefficient, Qf, is omitted from Eq. (J10-4). Qf is intended for connections where forces are normal to the HSS wall compressive stress. In this cap plate connection, the compressive force is parallel to the compressive stress in the HSS wall.
Below is a summary of variables to assume in Specification Eq. (J10-4):
Fyw=Fy of HSS Column
tf=Cap plate thickness, tp
tw=HSS wall thickness, tdes
lb=Transverse Plate or Web Thickness
d=B/2
Qf is omitted
Incorporating these variables into AISC 360-16 Specification Eq. (J10-4) results in the nominal strength based on HSS wall local crippling, for one wall:
For (5tb+ lb) < B:
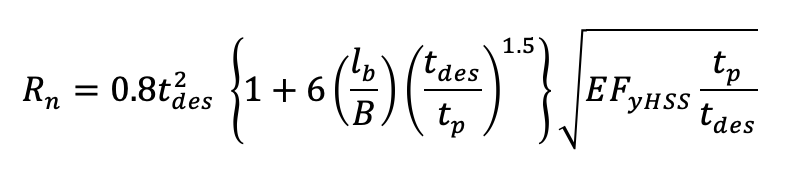
Φ = 0.75,Ω = 2.00
(5tb+ lb) < B as discussed above, then two rectangular HSS walls are engaged to resist local crippling due to the axial compressive force. Therefore, Rn per Eq. (4) is doubled to account for two HSS walls resulting in Eq. (5). This equation is consistent with AISC 360-10 Specification Eq. (K1-15). If (5tb + lb) > B, all 4 HSS walls are engaged and local crippling will rarely govern over local yielding.
For the limit state of HSS wall local crippling, for two walls:
(5tp+ lb) < B:
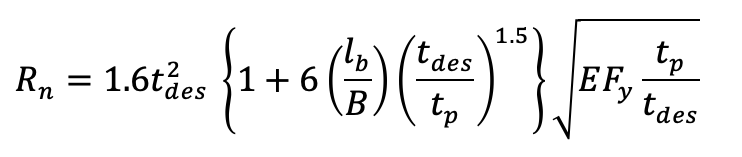
Φ = 0.75,Ω = 2.00
Beam Over HSS Column Connection with Moment
Note that this limit state is also applicable for beam over rectangular HSS column joints in which moment is transferred across the beam-to-column interface.
Assuming that (5tb + lb) < B, then two HSS walls contribute to resisting the applied beam moment, resulting in one HSS sidewall to resist the compression couple force. Therefore, Eq. (4) for one wall shall be applied to determine the local crippling capacity of the HSS column.
References
AISC. 2010a. “Steel Design Guide Series 24: Hollow Structural Section Connections”, American Institute of Steel Construction, Chicago, IL.
AISC. 2010. “Specification for Structural Steel Buildings”, ANSI/AISC 360-10, American Institute of Steel Construction, Chicago, IL.
AISC 2011. “Steel Construction Manual, Fourteenth Edition”, American Institute of Steel Construction, Chicago, IL.
AISC. 2016. “Specification for Structural Steel Buildings”, ANSI/AISC 360-16, American Institute of Steel Construction, Chicago, IL.
AISC. 2017. “Steel Construction Manual, Fifteenth Edition”, American Institute of Steel Construction, Chicago, IL.
CIDECT 2009. “Design Guide 3: For Rectangular Hollow Section (RHS) Joints Under Predominantly Static Loading 2nd Edition”, Comite International pour le Developpement et l’Etude de la Construction Tubulaire.
AISC 1997. “Hollow Structural Sections Connections Manual”, American Institute of Steel Construction, Chicago, IL.
February 2019