HSS Bollards
By Jeffrey A. Packer
Bahen/Tanenbaum Professor of Civil Engineering, University of Toronto, Ontario, Canada
Bollards are a familiar sight throughout the urban landscape. These short poles are used to protect infrastructure and to serve as a barrier, particularly to vehicles. They are used in design against blast loading, as a first line of defense, and are incorporated into any threat analysis; by keeping vehicles further away from any critical structure the standoff distance is increased, hence the magnitude of any blast loading originating from a vehicle-borne explosive is decreased. Even more common is the use of bollards to prevent the direct impact of vehicles on buildings or sensitive objects. Inside a structure (Figure 1(a)), they may be used to prevent accidental impacts from vehicles in car parks, or forklifts inside warehouses. Outside a structure (Figure 1(b)) their use is to prevent vehicles from access to certain routes or restricted areas, to guard buildings against intentional or accidental impact, and similarly to prevent impacts on equipment, facilities or assets.

Although bollards may be designed to be retractable, removable, or even decorative features (e.g. large concrete boxes containing plants or trees), the most common bollard is a simple, concrete-filled, HSS (Figure 2). Since these members are designed for impact resistance, round HSS are preferable to square HSS as the latter have a reduced Charpy V-notch (CVN) impact resistance in their four corners. ASTM A1085 (ASTM, 2015) would be the preferred HSS material as this requires a minimum CVN value of 25 ft-lb @ 40oF, which corresponds to AASHTO Zone 2. Furthermore, round HSS to ASTM A1085 have a minimum yield stress of 50 ksi. Since most bollards are located outdoors, hot-dip galvanizing is often required for environmental protection (Figure 1(b)), and round HSS are more readily galvanized than square or rectangular HSS too. Tubular bollards can also serve as an architectural complement to other exposed HSS construction (Figure 1(b)). The most common sizes used for bollards are outside diameters of 4.500 in. (which has limited capacity), 6.625 in. and 8.625 in. OD.
HSS bollards are usually designed as cantilever members and hence require fixity at the foundation. If mounted on a hard-finished surface via a bolted base-plate, as shown in Figure 1(a), the lateral load resistance will likely be limited by the baseplate connection. On the other hand, embedment in a foundation (Figure 2) can provide a high lateral load resistance and the member may be designed as a fixed-ended cantilever beam. This article deals with the design of the bollard itself, as a composite member, assuming full fixity at the base.

Design Approaches for Impact Loading
Eurocode 1 (CEN, 2006) categorizes structural impact by consequences of failure, and also by “hard impact” (where energy is mainly dissipated by the impacting body) versus “soft impact” (where the structure is designed to deform in order to absorb the impact energy). The key parameters influencing the impacting force on a bollard include the mass and stiffness of the vehicle and its velocity at impact. Herein, soft impact is assumed, thus the concrete-filled steel tube (CFST) member is assumed to deform to its full plastic moment capacity as a composite member. Hence, only compact sections according to AISC 360 Chapter I (AISC, 2016) are suitable. When calculating the plastic moment capacity the resistance factor can be taken as 1.0. Impact forces can be determined using a static equivalent approach or using an energy method involving plastic deformation of the “structure”. By using the static equivalent force method, a simple relationship between the lateral impact force and the maximum bending moment in the bollard can be used.
Static Equivalent Force Method
By considering only the first stage of impact, the vehicle stiffness is used to calculate the equivalent static force. A vehicle equivalent stiffness of 300 kN/m is adopted in Eurocode 1 Part 1.7 (CEN, 2006), for all types of vehicles and velocities at impact. The static equivalent impact force, in SI units, is then given by:
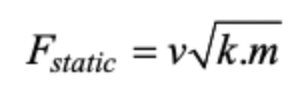
where v is the vehicle velocity at impact (in m/s), k is the vehicle equivalent stiffness (i.e. 300,000 N/m) given in EC1, m is the mass of the vehicle (in kg), and Fstatic is given in Newtons, N (CEN, 2006). Knowing the equivalent static force, the maximum bending moment produced in the bollard (at the base of the cantilever) is simply (Fstatic).h, where h is the height above ground of the point of impact, which may be taken as approximately 0.5 m (1.6 ft.) for cars and 1.5 m (5 ft.) for full-size trucks. Table 1 may be used as a guide to vehicle mass. Finally, one needs to select a CFST such that its plastic moment capacity exceeds the maximum bending moment developed at the base of the bollard.
Table 1: Approximate mass of vehicles (Zhao et al., 2019)
| Type of Vehicle | Mass Range (in kg) | Mass Range (in lb) |
| Small car | 1000 to 1500 | 2200 to 3300 |
| Minivan | 1500 to 3000 | 3300 to 6600 |
| SUV | 2000 to 3500 | 4400 to 7700 |
| Mini-bus | 3000 to 5500 | 6600 to 12000 |
| Bus | 10000 to 18000 | 22000 to 40000 |
| Two-axle truck | 6000 to 15000 | 13000 to 33000 |
| Three-axle truck | 9000 to 25000 | 20000 to 55000 |
| Four-axle truck | 10000 to over 30000 | 22000 to over 66000 |
Design Example
Determine the size of bollard required to resist impact from a large SUV, or similar, in a car park, travelling at 20 mph. A Cadillac Escalade has a curb weight of 5800 lb., so allow for 6600 lb. or 3000 kg. (see Table 1). A speed of 20 mph (x 1.61) = 32.2 kph = 32,200 m/h = 9 m/s. Thus, using Eq. (1):
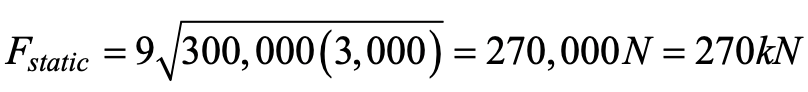
Thus, an impact force of 270 kN (x 0.225) = 60.8 kips can be assumed to be applied at 0.5 m (1.64 ft.) above ground level, creating a bending moment of 135 kNm (x 0.738) = 100 kip-ft. at the base of the bollard. Try an HSS 8.625 x 0.313 ASTM A1085, with a yield stress of Fy = 50 ksi, filled with normal-density concrete having fc/ = 6 ksi. First, check that the composite round HSS selected is compact, per AISC 360-16 Table I1.1b:
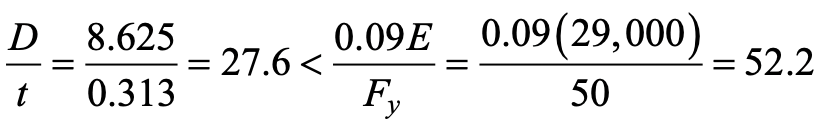
The plastic moment capacity of the composite member in flexure may be calculated using Table 6-5 of the AISC Manual (AISC, 2017). For the axial force vs. moment interaction diagram given in Table 6-5, point B designates the moment-only case. Using the notation and method (which is based on the assumption of a thin HSS wall) in that Table,
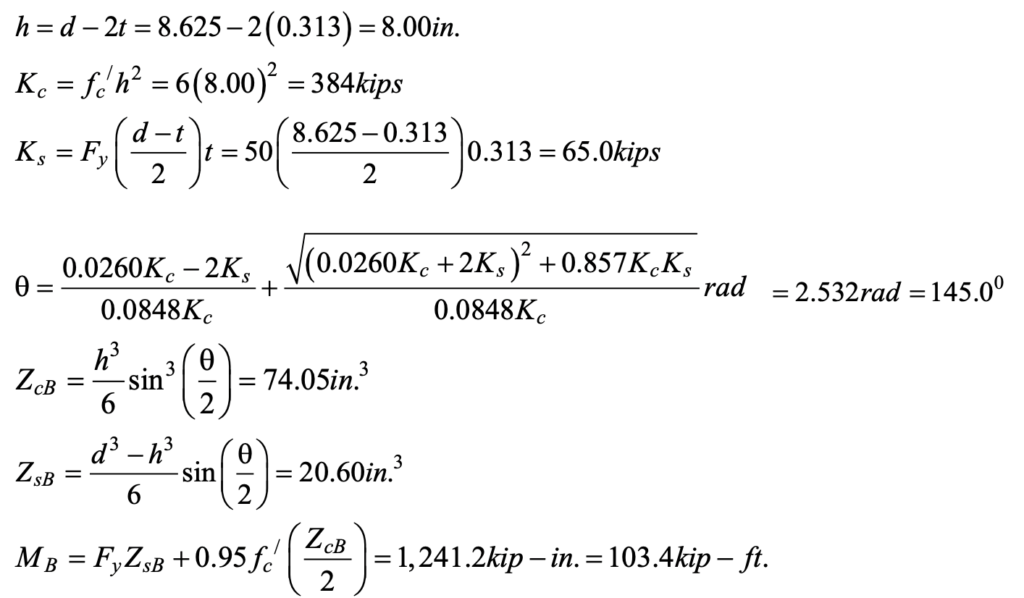
This plastic moment capacity, MB > 100 kip-ft., hence the bollard design is adequate. Zhao et al. (2019) Table 5.3(a) provides a list of plastic moment capacities, for many round HSS sizes with concrete filling (having similar material strengths as this example). This table is in SI units and moment capacity is computed based on Elchalakani et al. (2001), but it can serve as a good guide for sizing.
References
AISC. 2016. “Specification for Structural Steel Buildings”, ANSI/AISC 360-16, American Institute of Steel Construction, Chicago, IL.
AISC. 2017. “Steel Construction Manual”, 15th Edition, American Institute of Steel Construction, Chicago, IL.
ASTM. 2015. “Standard Specification for Cold-Formed Welded Carbon Steel Hollow Structural Sections (HSS)”, ASTM A1085/A1085M-15, American Society for Testing and Materials International, West Conshohocken, PA.
CEN. 2006. “Actions on Structures – Part 1-7: General Actions – Accidental Actions”, EN 1991-1-7, European Committee for Standardization, Brussels, Belgium.
Elchalakani, M., Zhao, X.-L. and Grzebieta, R.H. 2001. “Concrete-Filled Circular Steel Tubes Subjected to Pure Bending”, Journal of Constructional Steel Research, Vol. 57, No. 11, pp. 1141-1168.
Zhao, X.-L., Packer, J.A., Wang, Y.C. and McCormick, J.P. 2019. “Design Guide for Concrete-Filled Hollow Section Columns under Static, Impact, Blast, Seismic and Fire Loading”, CIDECT Design Guide No. 10, CIDECT, Geneva, Switzerland.
September 2021