Effects of Slender Elements in HSS Compression Members
By Mike Manor, PE, MLSE
FORSE Consulting, Technical Consultant to the Steel Tube Institute
Introduction
Hollow structural sections (HSS) are commonly used in buildings as columns to support compression forces from floor and roof loads. HSS members start as a hot-rolled steel plate which is then cold-formed into round, square or rectangular tube shapes with the edges welded together. These tubes are considered “closed” shapes due to the continuous nature of the walls; thus, there is no “end” to the cross section. Closed shapes in compression are a more efficient use of material compared to open shapes, such as wide flanges. In other words, thin, closed steel shapes will provide the same capacity as an open shape with less total material. However, when the wall thickness is thin compared to its width, additional failure modes are introduced that can limit the column capacity. This article will discuss the impacts of thin sections on the capacity of HSS column shapes.
Column Capacity Criteria
The strength of a column is based on the lowest available strength between yielding and buckling. Yielding is the point at which steel moves from being an elastic material to deforming in an inelastic manner and will no longer return to its original shape. Buckling occurs when there is a sudden change in geometry of the steel member, either globally or locally, of which there are four possible buckling modes: flexural buckling, torsional buckling, flexural-torsional buckling and local buckling.
Global Buckling
Flexural buckling occurs at the global level when the compression member deflects laterally about principal axis without twist or change in shape (refer to Figure 1(a)). The capacity for flexural buckling can be determined by Euler’s formula as incorporated in AISC 360-16 Equation E3-4. Torsional buckling is another global buckling mode that occurs when a member twists about its shear center axis (Figure 1(b)). This buckling mode is applicable to open cross sections. Due to the high torsional resistance of the closed shapes, HSS members do not need to be checked for this buckling mode. Flexural-torsional buckling is the third global buckling mode, which happens when a compression member simultaneously twists and deflects laterally (Figure 1(c)). Essentially, this buckling mode is a combination of the previous two and, again, this buckling mode is not relevant to HSS shapes. These three global buckling modes affect the capacity of the column based on the member geometry as a whole. In each case, the cross section remains the same.
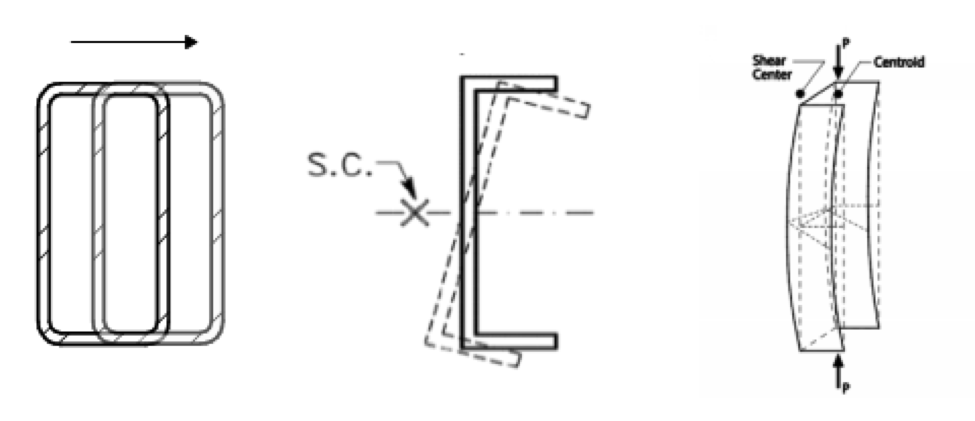
Figure 1 — Column Global Buckling Modes
(AISI S100-12 Commentary)
Local Buckling
In contrast, the final buckling mode, local buckling, occurs when one or more segments of the cross section buckle, changing the shape of the cross section. It is possible for these individual segments to buckle prior to global buckling, resulting in a reduction of the overall column capacity. The key criterion for determining local buckling is the width-to-thickness ratio (λ) of each element within the cross-sectional shape. AISC 360-16 Table B4.1a shows the limiting values (λr) that determine when local buckling must be considered. For each individual element of the cross section, if λ is less than or equal to λr, these elements are considered “non-slender” and local buckling will not occur. However, when λ is greater than λr, these elements are “slender” and local buckling must be considered when determining the column capacity. As discussed earlier, HSS members often use thinner steel thicknesses than other steel shapes. HSS have high values of λ and local buckling has an increased chance of controlling the column capacity.
When evaluating local buckling in a shape’s cross section, there are two types of elements to consider. The first is called an unstiffened element (Figure 2(a)). This means that the straight portion of the element is only connected to the rest of the cross section through a stiffer element on one end.
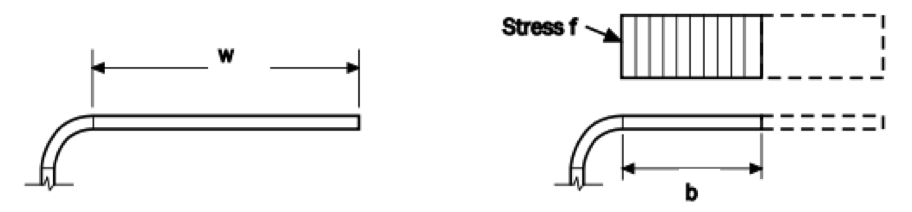

Figure 2 — Shape Cross-Sectional Elements and Effective Widths
(AISI S100-12)
An example of this would be the flange of wide flange or channel shapes. When in compression, the unstiffened edge of the element will start to buckle locally at much lower stresses than the stiffened edge. The second type of cross-section element to consider is called a stiffened element (Figure 2(b)), which is attached to a stiffer element on both edges. Examples of stiffened elements are webs of wide flanges, any side of a rectangular HSS member or the perimeter of round HSS. Stiffened elements are restrained from buckling on both ends, which means that buckling must occur at the middle of the element (Figure 3(a)).
When global buckling modes occur, the result is immediate loss of strength from the entire cross section, which can result in collapse. In contrast, when the local buckling stress of a stiffened element is reached, a redistribution of the stresses occurs followed by the ability to support additional load beyond the point of buckling. This phenomenon is known as “post-buckling strength.” The mechanism for how post-buckling strength works is shown graphically in Figure 3(a). When the plate buckles under the compressive load, the center of the plate moves perpendicularly outward. Since the plate is still attached at the edges, the plate develops horizontal tensile stresses that resist the full buckling behavior, which provides additional strength beyond the compressive buckling capacity. One note specific to rectangular HSS columns is the flanges of the HSS on all sides are continuous and cannot buckle in the same direction for the entire length. Looking at one point on an HSS column (Figure 2(b)) under a compressive load, two of the sides across from each other will buckle concavely and the other two sides will buckle convexly. Additionally, along the length of the HSS column as well as all other stiffened elements, the continuity of the steel will buckle in alternate directions, creating a sinusoidal buckling pattern (Figure 3(b)).
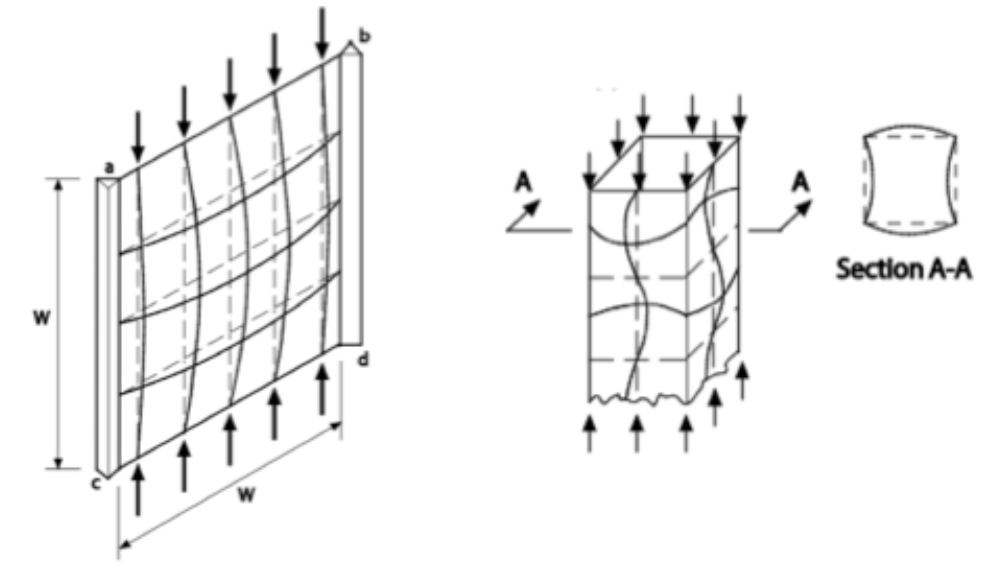
Figure 3 — Stiffened Element With Post-Buckling Strength
(AISI S100-12 Commentary)
To calculate the post-buckling strength, we need to start with the original steel shape at low stress levels. Prior to buckling, the compressive stress in the plate is uniform (Figure 4(a)), but after buckling, a portion of the stress at the middle of the plate transfers to the outer edges of the plate (Figure 4(b)). The stress continues to redistribute until the outer portions of the plate reach the yield stress of the steel (Figure 4(c)), at which point the plate begins to fail.
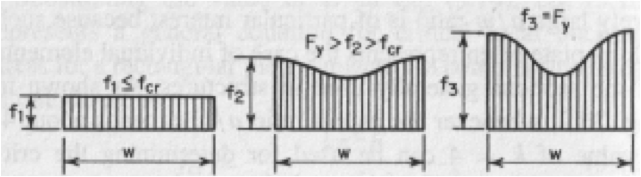
Figure 4 — Plate Stresses in Stiffened Element
(Cold-Formed Steel Design, 4th Edition)
The post-buckling behavior can be analyzed using large deflection theory and differential equations. However, due to the complexity, the solutions to these differential equations are not applicable to practical design. To approximate and simplify the solution, the concept of an effective width (Figures 2 and 5) is used for design purposes. The effective width “b” is determined such that the area under the nonuniform stress curve is equal to the sum of the two rectangular dashed parts in Figure 5. In essence, “b” is the width of the plate that buckles at the same time the maximum stress reaches the yield stress.
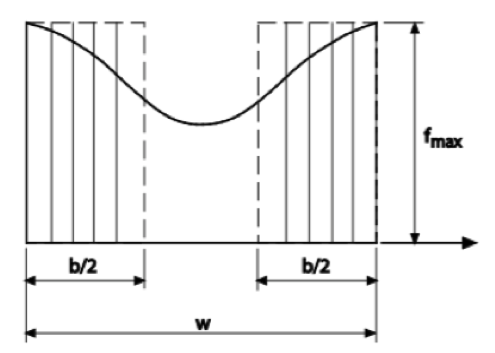
(AISI S100-12 Commentary)
There is one last piece of the puzzle remaining. Prior to this point, the global and local buckling modes have been discussed as separate limit states. The reality is they are interactive. The point at which a slender element begins to influence column strength is
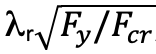
with Fcr being the lowest critical stress determined from global buckling modes in Sections E3 and E4 of AISC 360-16. Note that this is a change from previous editions of AISC 360 where the Q-factor method was used in place of the effective width method described above. The Q-factor method did rely on effective widths for stiffened elements only, but they were based on using the actual column stress in an iterative process or with Fy as a conservative lower bound approach. The Q-factor method was successful, but further research has shown it to be quite conservative in many cases.
Returning to the discussion of AISC 360-16, all slender elements, stiffened and unstiffened, have been generalized into a single set of equations in Section E7. The effective width of each element within the cross section must be calculated separately and then multiplied by the steel thickness to determine the total effective area for the cross section. Finally, the column capacity is calculated by multiplying the total effective cross-sectional area with the global buckling critical stress and applicable ASD/LRFD factors.
Round HSS Columns
Round HSS column shapes are also commonly used as compression members, such as columns. In evaluating the strength of round HSS, flat plate buckling theory is not appropriate; however, AISC 360-16 Section E7.2 similarly calculates column strength capacity using an effective cross-sectional area when classified as a slender element per Table B4.1a. Based on testing, the classical theory of compressed cylinders greatly overestimates the compressive capacity, often by more than 200%. The culprit for this discrepancy is imperfections of the cross-sectional shape which lead to unintentional eccentricities and a decrease in the actual column capacity. Therefore, to account for this reduction in capacity as well as the interaction of global and local buckling, only a portion of the cross-sectional shape is considered effective. The equation given by the specification for the effective area is based on testing rather than theoretical calculations. Additionally, the upper limit on the ratio of shape diameter to thickness is based on testing observations and AISC does not recommend using round HSS column shapes above that limit.
Concluding Notes for HSS Columns
The discussion above on slender column capacities provides the background to understand the implications of using thin-walled rectangular HSS as columns. In rectangular HSS columns, all four tube wall segments are stiffened elements, which can have higher width-to-thickness ratios than unstiffened elements. HSS columns can use less steel when compared to wide flange or other shapes. They take advantage of the post-buckling strength for larger effective widths to make use of a higher percentage of the total shape cross-sectional area. Additionally, the torsional properties of HSS allow for higher column heights based on global buckling limit states. Ultimately, this means that HSS columns provide a very efficient use of steel for building columns.
References
AISC, 2010. “Specification for Structural Steel Buildings”, ANSI/AISC 360-10, American Institute of Steel Construction, Chicago, IL.
AISC, 2011. “Steel Construction Manual, Fourteenth Edition”, American Institute of Steel Construction, Chicago, IL.
AISC, 2016. “Specification for Structural Steel Buildings”, ANSI/AISC 360-16, American Institute of Steel Construction, Chicago, IL.
AISC, 2017. “Steel Construction Manual, Fifteenth Edition”, American Institute of Steel Construction, Chicago, IL.
AISI, 2012. “AISI S100-12 North American Specification for the Design of Cold-Formed Steel Structural Members”, American Iron and Steel Institute.
STI, 2015. “HSS Design Manual, Volume 1: Section Properties & Design Information”, Steel Tube Institute.
STI, 2016. “HSS Design Manual, Volume 2A: Member Design”, Steel Tube Institute.
Yu, Wei-Wen & Roger LaBoube, 2010. “Cold-Formed Steel Design, Fourth Edition,” John Wiley & Sons, Hoboken, NJ.
September 2019