Deep Dive into HSS Shear and Moment Connection Examples
By Brady Golinski, PE; Mike Manor, PE; and Cathleen Jacinto, PE, SE
Technical Consultants, Steel Tube Institute
HSS is commonly utilized as a column or truss member due to its efficiency to transfer axial and torsional forces in a structure. To illustrate how to design connections to HSS members, we will dive into HSS connection examples for one common connection type and one less common connection that is difficult to find an example for in current AISC publications. Using AISC 360-2016 Specification and the 15th Edition Manual as a basis, we will step through an example for the HSS connections below. References are also made to the Steel Tube Institute’s Limit State Tables that can be downloaded here. The Limit State Tables summarize HSS local limit states to consider when designing HSS connections and outline design equations in the AISC Specification and Manual with variable substitutions specific to HSS.
- WF Beam to HSS Column Single Plate Shear Connection
- HSS-to-HSS Connection With Shear, Axial and In-Plane Moment
WF Beam to HSS Column Single Plate Shear Connection Example
The following example is a WF beam-to-HSS column single plate connection resisting shear. Design the connection per the AISC 360-16 Specification and AISC 15th Edition Manual. Loads shown are factored per LRFD load combinations.
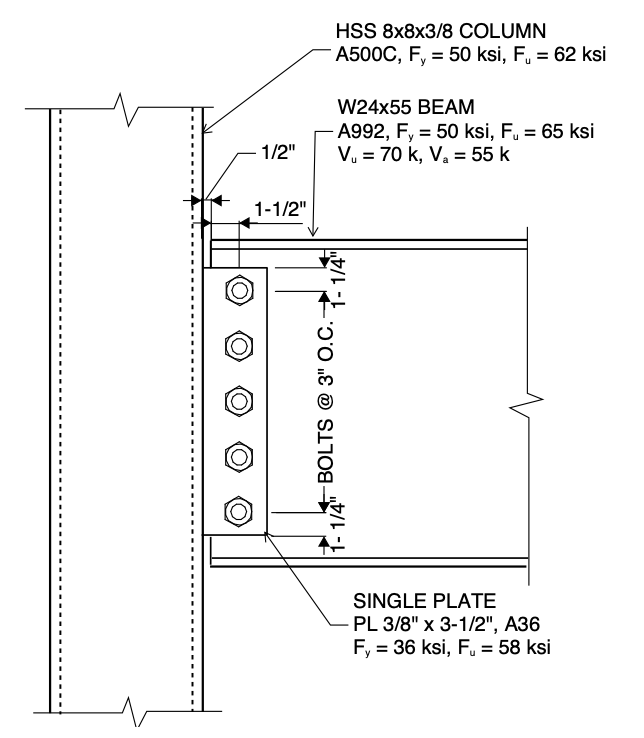
| HSS8x8x3/8 Column: | W24x55 Beam: | Bolts: |
| ASTM A500 Grade C Fy = 50 ksi Fu = 62 ksi H = 8 in B = 8 in tdes = 0.349 in A = 10.4 in2 Sx = 24.9 in3 | ASTM A992 Fy = 50 ksi Fu = 65 ksi tw = 3/8 in T = 20 ¾ in | ¾” diameter A325-N STD holes in beam SSLH holes in plate |
Determine the capacity of the WF beam-to-HSS column single plate connection. Note there are a number of alternate shear connections that can be utilized and are discussed in this article. A through-plate shear connection is one other shear connection option in which the single plate extends through slots in the HSS column both near side and far side. However, the through-plate connection is a more costly connection to fabricate. The single plate is typically the most cost-effective connection to resist shear.
Per AISC 15th Edition Manual page 9-17, to ensure rotational ductility in the single plate connection, the geometry and thickness of the plate are configured so that the plate will yield, the bolt group will rotate, and/or the bolt holes will elongate at failure prior to failure of welds or bolts. Per the AISC 15th Edition Manual page 10-88, check that the following dimensional limitations are met to ensure the single plate connection is consistent with a conventional configuration.
- There is only a single row of bolts, 2 ≤ n ≤ 12
- The distance from the bolt line to the weld line a = 2 in ≤ 3 1⁄2 in OK
- Standard or short-slotted holes are used
- lev = 1.25 in ≥ 1 in (from AISC 360-16 Table J3.4), leh = 1.5 in ≥ 2d = 1.5 in OK
- tp = 0.375 in ≤ d⁄2 + 1⁄16 = 0.4375 in OK
Since all conditions are met, this connection can be designed as a conventional configuration.
We refer to the Steel Tube Institute’s Limit State Tables to determine the limit states to check per AISC 360-16 Specification and the 15th Edition Manual. Figure 2 shows an excerpt from the Shear Limit State Tables Single Plate Connection.
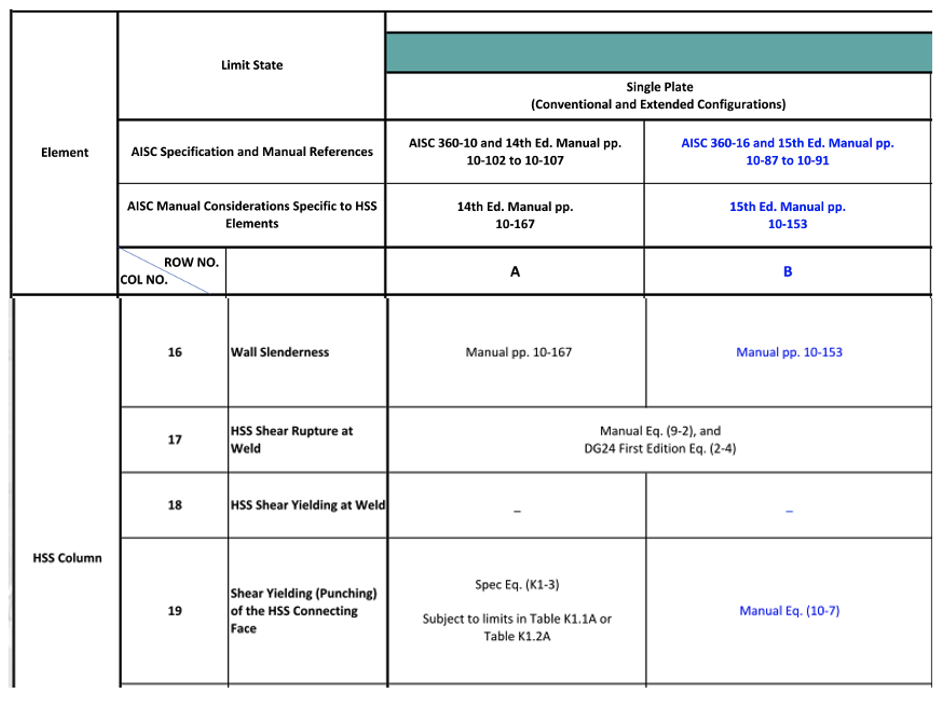
1. Bolt Shear (Limit State Table Cell B2, Shear)
¾” A325N Bolts
ɸrn = 17.9 k/bolt [AISC 15th Edition Manual Table 7-1]
a = 2 in, e = a/2 = 2 in/2 = 1 in
5 bolts
C = 4.77
ɸRn = Cɸrn = 4.77(17.9) [AISC 15th Edition Manual Table 7-6]
85.4 k > 70 k OK
The “T” dimension of a W24x55 is 20 ¾”
AISC 15th Edition Manual page 10-7 recommends a minimum connection length of T/2
Plate vertical dimension is Lc = (2)(1¼”)+(4)(3″) = 14½” < 20 ¾” OK
Lc = 14½” > T/2 = 20.75”/2 = 10.375” OK
2. Bolt Bearing and Tearout in the Plate and Beam Web (Limit State Table Cell B4, Shear)
Since the connection geometry meets the requirements for the conventional configuration, the plate bearing and tear-out checks may be calculated with the load applied as concentric per AISC 15th Edition Manual page 10-89. Consider deformation at the bolt hole at service loads. Since the plate and W24x55 beam web thickness are both 3/8 inch, the plate calculations below can also be applied to the W24 beam web.
Bearing Rn = 2.4dtFu [AISC 360-16 Equation J3-6a]
Rn = 2.4 × 0.75 in × 0.375 in × 58 ksi = 39.1 k/bolt
Tear-out: Rn = 1.2lc tFu [AISC 360-16 Equation J3-6c]
At bottom bolt:
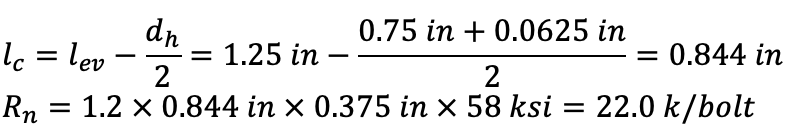
At other bolts:
lc = s – dh = 3 in – (0.75 in + 0.0625 in) = 2.19 in
Rn = 1.2 × 2.19 in × 0.375 in × 58 ksi = 57.0 k/bolt
At the bottom bolt, tear-out controls; at the other bolts, bearing controls. Therefore:
ϕRn = 0.75 × (22.0 k⁄bolt + 4 × 39.1 k⁄bolt) = 134 k > Ru=70 k OK
3. Plate Shear Limit States (Limit State Table Cells B5, B6 and B10, Shear)
Shear Yield
Rn = 0.60FyAgv [AISC 360-16 Equation J4-3]
Agv = 14.5 in × 0.375 in = 5.44 in2
ϕRn = 1.0 × 0.60 × 36 ksi × 5.44 in2 = 117 k > Ru=70 k OK
Shear Rupture
Rn = 0.60FuAnv [AISC 360-16 Equation J4-4]
Anv = 0.375 × [14.5 in – 5 × (0.75 in + 0.125 in)] = 3.80 in2
ϕRn = 0.75 × 0.60 × 58 ksi × 3.80 in2 = 99.1 k > Ru = 70 k OK
Block Shear Rupture
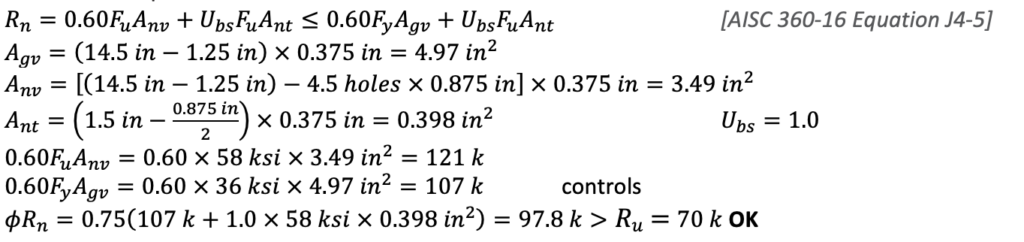
4. Weld Strength (Limit State Table Cell B14, Shear)
AISC 15th Edition Manual page 10-87 offer guidance on sizing the weld between the single plate and the supporting member, our HSS column, to be 5/8tp. This develops the strength of the plate to ensure the weld is not the critical limit state. For our 3/8 inch thick single plate:
Weld size, w= 5⁄8 tp = 0.625 × 0.375 in = 0.234 in
Therefore, try 1/4″ fillet welds, each side of plate.
Check weld shear capacity (fillet weld on each side of the plate):

5. HSS Column Slenderness (Limit State Table Cell B16, Shear)
Confirm the HSS8x8x3/8 column selected is not classified as a slender element per AISC 360-16 Specification Table B4.1a Case 6 and 15th Edition Manual page 10-153.
For rectangular HSS sections:
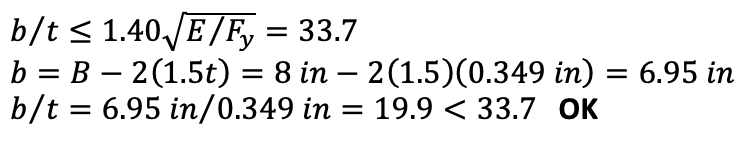
Note that the resulting b/t ratio is consistent with the AISC 15th Edition Manual Table 1-12 tabulated value for b/t for the HSS8x8x3/8 section.
6. Shear Yielding (Punching Shear) of the HSS Wall (Limit State Table Cell B19, Shear)
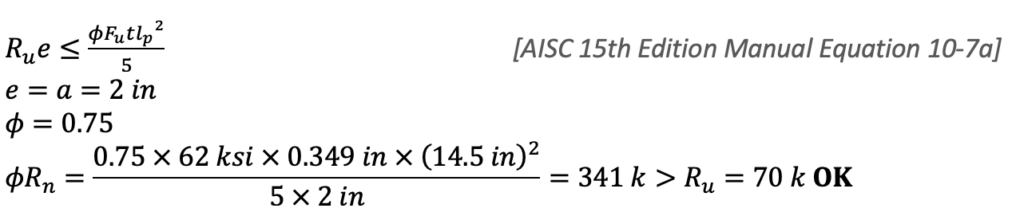
7. Shear Rupture at Weld (Limit State Table Cell B17, Shear)
In welded joints, the AISC Specification requires that both the weld metal and base metal be checked. Specifically for HSS, we must check that the HSS wall thickness is sufficient to adequately transfer the shear along the length of the weld, which is 14.5 inches.
Rn = 0.6FuAnv [AISC 360-16 Equation J4-4]
ϕ = 0.75
ϕRn = 0.75(0.6)(62 ksi)(2 sides)(0.349 in)(14.5 in) = 282 k > Ru =70 k OK
Alternately, determine the minimum HSS column thickness required to match the 1/4-inch fillet weld strength.
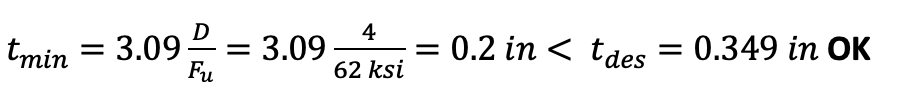
Therefore, the HSS8x8x3/8 column is adequate to transfer shear Vu = 70 kips at the connection.
The Steel Tube Institute’s HSS Connex tool performs the above HSS limit state checks #5 and #6. HSS Connex does not check the plate, bolts or welds, but it can assist in ensuring the HSS wall is adequate for its local limit states. Figure 3 shows output from HSS Connex for the connection in this example.

HSS-to-HSS Connection With Shear, Axial and In-Plane Moment Example
With the increasing prevalence of HSS branches connecting to HSS chords in structural applications – such as trusses, girt connections, cantilevers, and exposed steel structures – finding clear examples for HSS-to-HSS connections, especially for moment transfer, can be challenging. This example illustrates an HSS column supporting a cantilever HSS beam with a back span and an axial lateral pass-through force. The connection design follows AISC 360-16 Specification and 15th Edition Manual, with factored per LRFD load combinations.
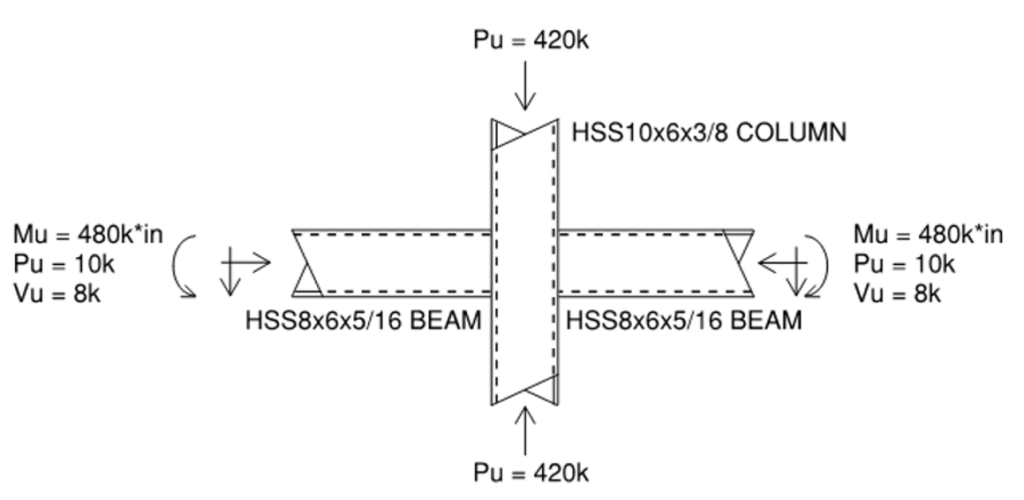
| HSS10x6x3/8 Column/Chord: | HSS8x6x5/16 Branch: |
| ASTM A500 Grade C Fy = 50 ksi Fu = 62 ksi H = 10 in B = 6 in tdes = 0.349 in A = 10.4 in2 Sx = 27.4 in3 Zx = 33.8 in3 | Fy = 50 ksi Fu = 62 ksi Hb = 8 in Bb = 6 in tb,des = 0.291 in Ab = 7.59 in2 Sb,x = 17.1 in3 Zb,x = 20.6 in3 |
Based on geometry, this connection is classified as a cross-connection with an in-plane moment. The column is the through member and is considered the “chord,” while the beams are considered the “branches.” Since the width of the chord and branches are the same, this is a matched width connection, i.e., β = 1.0 (Bb = B). This can be considered a fully restrained (FR) moment connection per AISC terminology. FR moment connections are considered sufficiently rigid, which means the change in angle between members when load is applied is negligible. In contrast, partially restrained (PR) connections can transfer moment, but the change in angle is not negligible and must be considered in the frame analysis per AISC section B3.4b(b).
AXIAL FORCE LIMIT STATES
1. HSS Chord Plastification (Limit State Table cell L1, Truss)
This is checked with AISC 15th Edition Manual Equation 9-30.
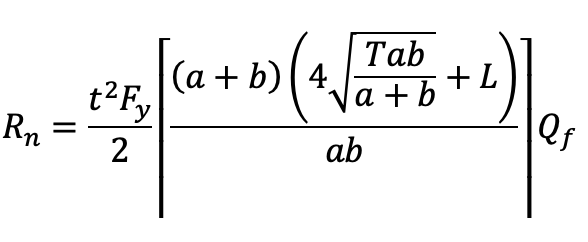
Refer to AISC 15th Edition Manual Figure 9-5(a). Since both the chord and the branch have a width of 6 inches, both a and b will equal zero, and therefore equation 9-30 is undefined. This makes sense since plastification occurs within the chord wall, but in this case, the branch has the same width. Therefore, the axial load transfers directly into the stiffer chord sidewalls instead of through the chord face, and this limit state is not applicable.
2. HSS Chord Shear Yielding (Punching) (Limit State Table Cell L2, Truss)
This is checked with AISC 15th Edition Manual equation 9-29.
Rn = 0.6Fy tp (2ceff + 2L)
This limit state occurs when the branch punches through the connecting face of the chord as a shear failure. Similar to plastification, the chord and branch have the same width in this example, which means a shear failure through chord cannot occur since the load will pass directly into the sidewalls. Therefore, this limit state is not applicable.
3. Local Yielding of HSS Chord Sidewalls (Limit State Table Cell L3, Truss)
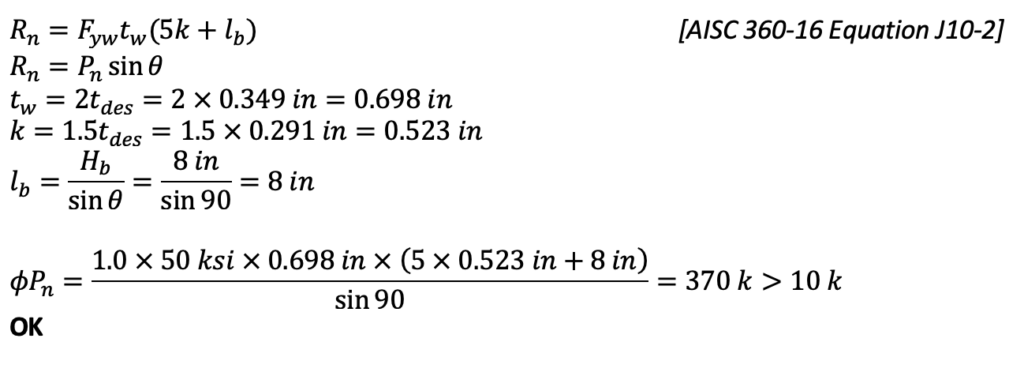
4. Local Crippling of HSS Chord Sidewalls (Limit State Table Cell L4, Truss)

5. Local Buckling of HSS Chord Sidewalls (Limit State Table Cell L5, Truss)

6. Local Yielding of HSS Branches Due to Uneven Load Distribution (Limit State Table Cell L6, Truss)
This limit state occurs because the chord face that the branch is attaching to has higher stiffness near the chord sidewalls than at the middle of the chord face. To account for this, an effective width is used for the branch walls perpendicular to the chord. Only the effective area will be counted on as shown in figure 5.
Effective area:
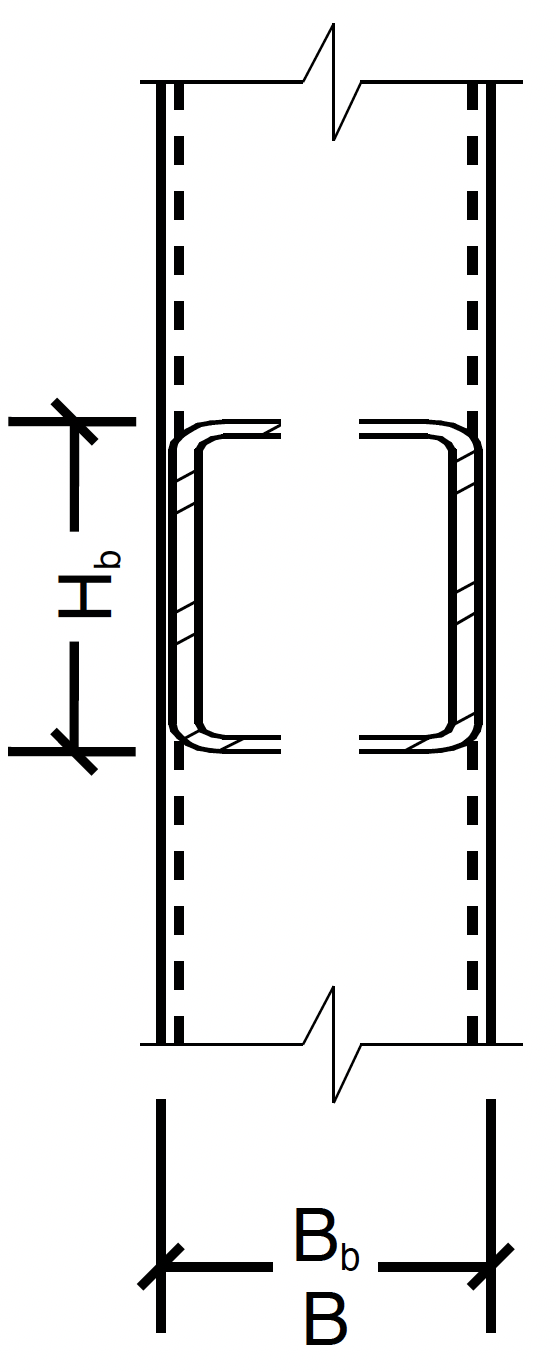
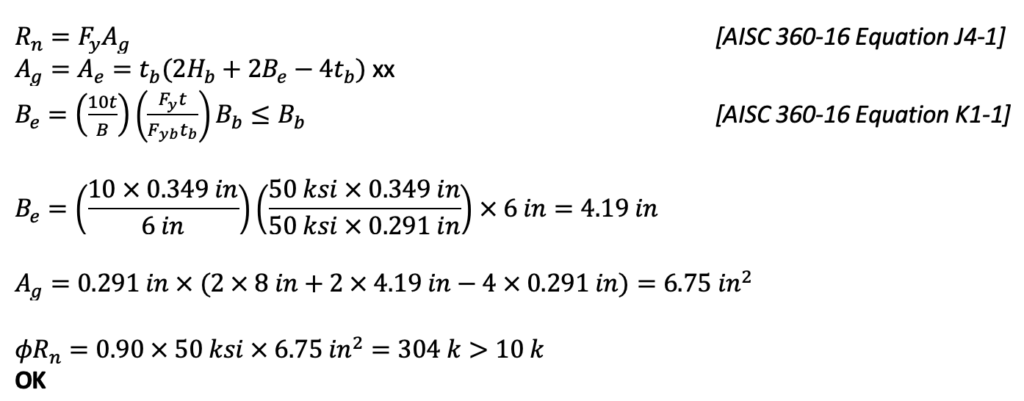
7. Shear Yielding of HSS Chord Sidewalls (Limit State Table Cell L7, Truss)
This limit state applies only for inclined branches. Since θ = 90 degrees in this example, there is no projected gap, and thus this limit state is not applicable.
Controlling Axial Limit State:
Local buckling of chord sidewalls: ϕRn = 241 k
MOMENT FORCE LIMIT STATES
1. Chord Wall Plastification (Limit State Table Cell F1, Moment)
This is checked with AISC 15th Edition Manual Equation 9-32.
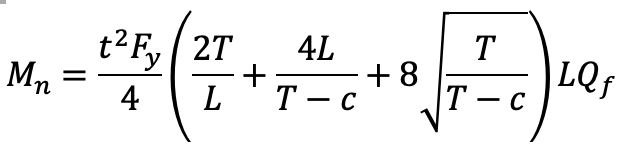
Referring to AISC 15th Edition Manual Figure 9-5(b), T = B and c = Bb. Since T – c = 0 will be in the denominator, equation 9-32 is undefined. Similar to item A1 under the axial section above, the force will transfer directly into the chord sidewalls, and therefore this limit state does not apply.
2. HSS Chord Shear Yielding (Punching) (Limit State Table Cell F2, Moment)
This is another limit state that checks the connecting face of the HSS chord. Since this is a matched connection where the chord and branch widths are equal, this limit state does not apply. See item 2 in the axial section above for similar discussion.
3. Local Yielding of HSS Chord Sidewalls (Limit State Table Cell F3, Moment)
Rn = Fyw tw (5k + lb ) [AISC 360-16 Equation J10-2]
tw = k = tdes
lb = Hb
Mn = Rn × moment arm
moment arm = 0.5(Hb + 5k) = 0.5 × (8 in + 5 × 0.349 in) = 4.87 in
ϕMn = 1.0 × 50 ksi × 0.349 in × (5 × 0.349 + 8 in) × 4.87 in = 829 k – in > 480 k – in
OK
4. Local Buckling of HSS Chord Sidewalls (Limit State Table Cell F5, Moment)
Buckling of the sidewalls is a limit state that is only applicable to matched width (β=1.0) cross-connections when the moment is equilibrated by each branch of the cross-connection. The strength of the moment connection is increased by yielding in the adjacent tensile region. The hybrid compression buckling and tension-yielding behavior is accounted for with a local yielding check using a reduced yield strength of 0.8Fy with the same equation variable values as local yielding in moment section 3 above.
Rn = Fyw tw (5k + lb ) [AISC 360-16 Equation 10-2]
Use ϕMn from moment check 3 above.
ϕMn = 0.8 × 829 k – in = 663 k – in > 480 k – in
OK
5. Local Yielding of Branches Due to Uneven Load Distribution (Limit State Table Cell F6, Moment)
Mn = Mp = FyZ [AISC 360-16 Equation F7-1]
Z = Znet

This limit state occurs because the chord face that the branch is attaching to has higher stiffness near the chord sidewalls than at the middle of the chord face. Thus, the load is passed through the effective portions of the branch and an effective branch Zb is used in this equation, Zb,net (see Figure 6). A modification and derivation of this can be found in the paper “Stepped HSS T- and Cross-Connections Under Branch In-Plane and Out-of-Plane Bending” by Dr. Jeffrey Packer, available on the STI website. The following equation can be found there:
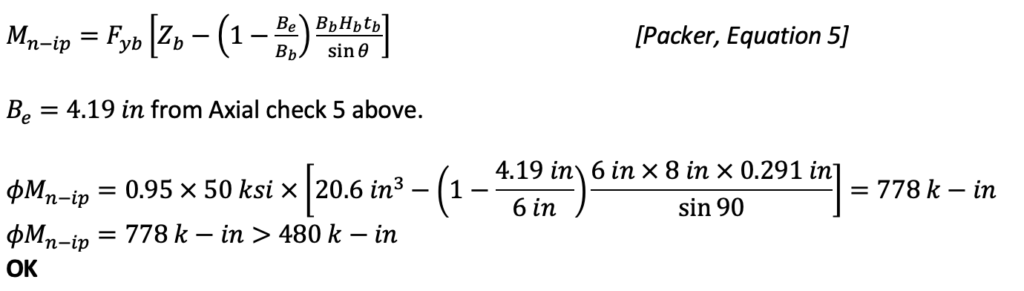
Controlling Moment Limit State:
Local buckling of chord sidewalls: ϕMn = 663 k – in > Mu = 480 k – in OK
AXIAL AND MOMENT INTERACTION

Therefore, this HSS-to-HSS moment connection is adequate to transfer the shear, axial and in-plane moment demand.
(NOTE: The zero term in the equation above reflects that there is no out-of-plane moment component in this example.)
February 2023
Utilizing Technology, Expertise and Communication for Better Connection Design Outcomes
Jerod Hoffman and Eric Corwin at Meyer Borgman Johnson talk with us about adapting emerging technologies within their steel connec…
ASCE 360-16 Limit State Tables
STI created Limit State Tables to help designers navigate the significant changes to Chapter K in the AISC 360-16 Specification. T…
Wide-Flange Beam to HSS Column Shear Connections and Applicable Limit States
Many of the same connections that are used for wide flange members can also be used for HSS members with occasional variations.